搜索
【题目】如图，抛物线y=ax2+bx+c与x轴交于点A（﹣1，0），B（4，0），与y轴交于点C（0，2），点D与点C关于x轴对称，点P是x轴上的一个动点，设点P的坐标为（m，0），过点P作x轴的垂线l，交抛物线于点Q．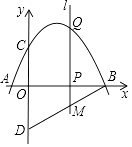
（1）求抛物线的解析式；
（2）求直线BD的解析式；
（3）当点P在线段OB上运动时，直线l交BD于点M，是否存在点P，使得四边形CQMD是平行四边形？若存在，求出m的值；若不存在，请说明理由．
参考答案：
【答案】
（1）
解：由题意可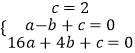得 
，解得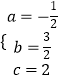 
，
∴抛物线解析式为y=﹣ 
x2+ 
x+2
（2）
解：∵点C与点D关于x轴对称，
∴D（0，﹣2），
∴可设直线BD解析式为y=kx﹣2，
把B（4，0）代入可得4k﹣2=0，解得k= ，
∴直线BD的解析式为y= x﹣2
（3）
解：如图所示，
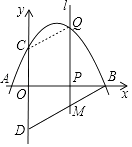
设Q（m，﹣ m2+ m+2），则M（m， m﹣2），
∴QM=﹣ m2+ m+2﹣（ m﹣2）=﹣ m2+m+4，
∵QM∥CD，
∴当QM=CD时，四边形CQMD是平行四边形，
∴﹣ m2+m+4=4，解得m=0（不合题意，舍去）或m=2，
∴当m=2时，四边形CQMD是平行四边形
【解析】（1）由A、B、C的坐标，利用待定系数法可求得抛物线的解析式；（2）由对称性可求得D点坐标，利用待定系数法可求得直线BD的解析式；（3）用m可表示出M、Q的坐标，则可表示出QM的长，由平行四边形的性质可知QM∥CD且QM=CD，则可得到关于m的方程，可求得m的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC经过一次平移到△DFE的位置，请回答下列问题：
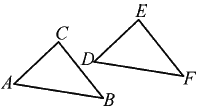
(1)点C的对应点是点__________，∠D=__________，BC=__________；
(2)连接CE，那么平移的方向就是__________的方向，平移的距离就是线段__________的长度；
(3)连接AD，BF，BE，与线段CE相等的线段有__________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图：
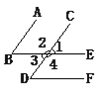
（1）如果∠1＝∠B，那么_______∥_______，根据是__________________________；
（2）如果∠3＝∠D，那么_______∥_______，根据是__________________________；
（3）如果要使BE∥DF，必须∠1＝∠_______，根据是_________________________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知在菱形ABCD中，∠ABC=60°，对角线AC、BD相交于点O，点E是线段BD上一动点（不与点B，D重合），连接AE，以AE为边在AE的右侧作菱形AEFG，且∠AEF=60°．
（1）如图1，若点F落在线段BD上，请判断：线段EF与线段DF的数量关系是.
（2）如图2，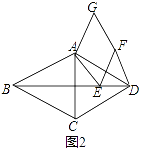
若点F不在线段BD上，其它条件不变，（1）中的结论是否仍然成立？请给出判断并予以证明；
（3）若点C，E，G三点在同一直线上，其它条件不变，请直接写出线段BE与线段BD的数系． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图是一个隧道的横断面，它的形状是以点O为圆心的圆的一部分，如果圆的半径为
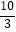m，弦CD=4m，那么隧道的最高处到CD的距离是（ ）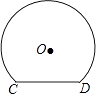 
A.
m
B.4m
C.
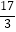m
D.6m -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，直线y=x+2与x轴交于点A，与y轴交于点C，与反比例函数y=
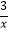在第一象限内的图象交于点B（1，3），连接BO，下面三个结论：①S△AOB=1.5，；②点（x1 ， y1）和点（x2 ， y2）在反比例函数的图象上，若x1＞x2 ， 则y1＜y2；③不等式x+2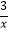＜ 的解集是0＜x＜1．其中正确的有（ ）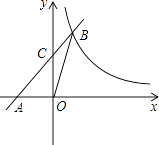 
A.0个
B.1个
C.2个
D.3个 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图(1)是一个长为2m，宽为2n的长方形，沿图中虚线剪成四个均匀的小长方形，然后按图(2)形状拼成一个正方形.
(1)你认为图(2)中的阴影部分的正方形的边长等于多少？
(2)观察图(2)，你能写出下列三个代数式之间的等量关系吗？代数式：
，
，
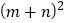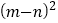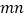；(3)已知：
，
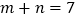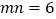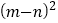，求的值.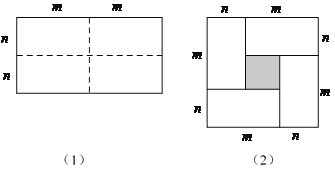
相关试题
