【题目】小明拿两个大小不等直角三角板作拼图，如图①小三角板的斜边与大三角板直角边正好重合，已知：AD=1，∠B=∠ACD=30°．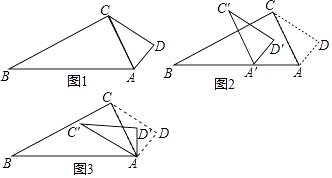

（1）AB的长；四边形ABCD的面积=（直接填空）；
（2）如图2，若小明将小三角板ACD沿着射线AB方向平移，设平移的距离为m（平移距离指点A沿AB方向锁经过的线段长度），当点D平移到线段大三角板ABC的边上时，求出相应的m的值；
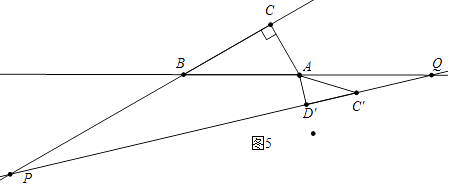
（3）如图3，小明将小三角板ACD绕点A顺时针旋转一个角α（0°＜α＜180°），记旋转中的△ACD为△AC′D′，在旋转过程中，设C′D′所在的直线与直线BC交于点P，与直线AB交于点Q，是否存在这样的P、Q两点，使△BPQ为等腰三角形？若存在，请直接求出此时D′Q的长；若不存在，请说明理由

参考答案：

【答案】
（1）4,
（2）解：如图2中，作DE∥AB交BC于E，交AC于F．

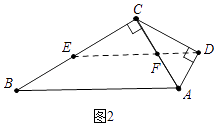
∴∠DFA=∠BAC=60°=∠DAF，

∴△ADF是等边三角形，

∴AF=AD=DF=CF=1，∵FE∥AB，

∴CE=EB，

∴EF= AB=2，

∴当点D平移到线段大三角板ABC的边上时，相应的m的值为1或3．


（3）解：①如图3中，当BP=BQ时，在AD′上取一点E使得AE=EQ．

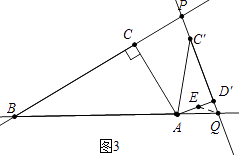
∵∠PBQ=30°，

∴∠AQD′=75°，∵∠AD′Q=90°，

∴∠EAQ=∠EQA=15°

∴∠QED′=30°，设D′Q=x，则AE=EQ=2x，ED′= x，

∴2x+ x=1，

∴x=2﹣ ，

∴D′Q=2﹣ ．

②如图4中，当BQ=PQ时，易知∠AQD′=60°，D′Q=ADtan30°= ．

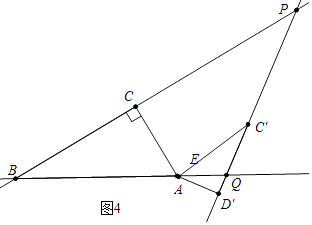
③如图5中，当BP=BQ时，易知∠AQC′=∠C′AQ=15°，∴AC′=C′Q，∴D′Q=D′C+C′Q′= +2．

综上所述，当△PBQ是等腰三角形时，D′Q的值为2﹣ 或 或 +2


【解析】解：（1）如图1中，

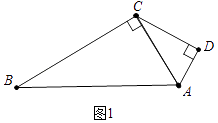
在Rt△ACD中，∵AD=1，∠ACD=30°，

∴AC=2CD=2，CD= AD= ，

在Rt△ACB中，∵∠B=30°，AC=2，

∴AB=2AC=4，BC= AC=2 ，

∴四边形ABCD的面积=S△ACD+S△ABC= + 22 = ．

所以答案是4， ．

【考点精析】解答此题的关键在于理解含30度角的直角三角形的相关知识，掌握在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半，以及对平行线分线段成比例的理解，了解三条平行线截两条直线，所得的对应线段成比例．

关闭