【题目】汽车租赁公司拥有某种型号的汽车100辆.公司在经营中发现每辆车的月租金x(元)与每月租出的车辆数(y)有如下关系:
x(元) | 3000 | 3200 | 3500 | 4000 |
y(辆) | 100 | 96 | 90 | 80 |
(1)观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识,求按照表格呈现的规律,每月租出的车辆数y(辆)与每辆车的月租金x(元)之间的关系式.
(2)已知租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.用含x(x≥3000)的代数式填表:
租出的车辆数(辆) | 未租出的车辆数(辆) | ||
租出每辆车的月收益(元) | 所有未租出的车辆每月的维护费(元) |
(3)若你是该公司的经理,你会将每辆车的月租金定为多少元,才能使公司获得最大月收益?请说明理由.
参考答案:
【答案】
(1)解:由表格数据可知y与x是一次函数关系,
设其解析式为y=kx+b.
由题: ![]() ,
,
解之得: 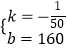 ,
,
∴y与x间的函数关系是y=﹣ ![]() x+160
x+160
(2)﹣ ![]() x+160,
x+160,![]() x﹣60,x﹣150,x﹣3000
x﹣60,x﹣150,x﹣3000
(3)解:设租赁公司获得的月收益为W元,依题意可得:
W=(﹣ ![]() +160)(x﹣150)﹣(x﹣3000)
+160)(x﹣150)﹣(x﹣3000)
=(﹣ ![]() x2+163x﹣24000)﹣(x﹣3000)
x2+163x﹣24000)﹣(x﹣3000)
=﹣ ![]() x2+162x﹣21000
x2+162x﹣21000
=﹣ ![]() (x﹣4050)2+307050
(x﹣4050)2+307050
当x=4050时,Wmax=307050,
即:当每辆车的月租金为4050元时,公司获得最大月收益307050元
【解析】解:(2)如下表:
租出的车辆数 | ﹣ | 未租出的车辆数 |
|
租出的车每辆的月收益 | x﹣150 | 所有未租出的车辆每月的维护费 | x﹣3000 |
所以答案是:﹣ ![]() x+160,
x+160, ![]() x﹣60,x﹣150,x﹣3000.
x﹣60,x﹣150,x﹣3000.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强学生的安全意识,某校组织了学生参加安全知识竞赛,从中抽取了部分学生成绩(得分数取正整数,满分为100分)进行统计,绘制统计图如下(未完成),解答下列问题:


(1)若A组的频数比B组小24,求频数分布直方图中的
 、
、 的值;
的值;(2)扇形统计图中,D部分所对的圆心角为n°,求n的值并补全频数分布直方图;
(3)若成绩在80分以上为优秀,全校共有2000名学生,估计成绩优异的学生有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知平行四边形ABCD,延长AD到E,使DE=AD,连接BE与DC交于O点.

(1)求证:△BOC≌△EOD;
(2)当△ABE满足什么条件时,四边形BCED是菱形?证明你的结论. -
科目: 来源: 题型:
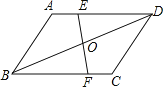
查看答案和解析>>【题目】已知:如图,在ABCD中,点E、F分别在AD、BC上,EF与BD相交于点O,AE=CF.
(1)求证:OE=OF;
(2)连接BE、DF,若BD平分∠EBF,试判断四边形EBFD的形状,并给予证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】填空并在后面的括号中填理由
如图,
 ,试问
,试问 、
、 、
、 有什么关系.
有什么关系.
解:
 .理由如下:
.理由如下:过点
 作
作
则
 _________(____________________________________)
_________(____________________________________)又∵
 (____________________________________)
(____________________________________)∴_________(____________________________________)
∴
 _________(____________________________________)
_________(____________________________________)∴
 (____________________________________)
(____________________________________)即
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.

(1)已知点M,N是线段AB的勾股分割点,若AM=2,MN=3,则BN=;
(2)如图2,在△ABC中,FG是中位线,点D,E是线段BC的勾股分割点,且EC>DE≥BD,连接AD,AE分别交FG于点M,N,求证:点M,N是线段FG的勾股分割点;
(3)如图3,已知点M,N是线段AB的勾股分割点,MN>AM≥BN,四边形AMDC,四边形MNFE和四边形NBHG均是正方形,点P在边EF上,试探究S△ACN , S△APB , S△MBH的数量关系.
S△ACN=;S△MBH=;S△APB=;
S△ACN , S△APB , S△MBH的数量关系是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形△ABC的腰长AB=AC=25,BC=40,动点P从B出发沿BC向C运动,速度为10单位/秒.动点Q从C出发沿CA向A运动,速度为5单位/秒,当一个点到达终点的时候两个点同时停止运动,点P′是点P关于直线AC的对称点,连接P′P和P′Q,设运动时间为t秒.

(1)若当t的值为m时,PP′恰好经过点A,求m的值.
(2)设△P′PQ的面积为y,求y与t之间的函数关系式(m<t≤4)
(3)是否存在某一时刻t,使PQ平分角∠P′PC?存在,求相应的t值,不存在,请说明理由.
相关试题

