【题目】在平面直角坐标系中,矩形OABC的边OA、OC分别落在x轴、y轴上,O为坐标原点,且OA=8,OC=4,连接AC,将矩形OABC对折,使点A与点C重合,折痕ED与BC交于点D,交OA于点E,连接AD,如图①. 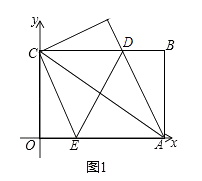
(1)求点D的坐标和AD所在直线的函数关系式;
(2)⊙M的圆心M始终在直线AC上(点A除外),且⊙M始终与x轴相切,如图②. 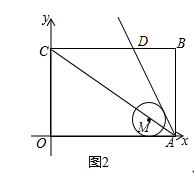
①求证:⊙M与直线AD相切;
②圆心M在直线AC上运动,在运动过程中,能否与y轴也相切?如果能相切,求出此时⊙M与x轴、y轴和直线AD都相切时的圆心M的坐标;如果不能相切,请说明理由.
参考答案:
【答案】
(1)解:设CE=t,
∵矩形OABC对折,使A与C重合(折痕为ED),OA=8,OC=4
∴CE=AE=t,∠AED=∠CED,
∴OE=OA﹣AE=8﹣t,
在Rt△OCE中,∵OE2+OC2=CE2,
∴42+(8﹣t)2=t2,
解得t=5,
即CE=AE=5
∵BC∥OA,
∴∠CDE=∠AED,
∴∠CDE=∠CED,
∴CD=CE=5.
∴D(5,4),
设直线AD的解析式 为y=kx+b,
将A(8,0)、D(5,4)代入解析式可得 ![]()
解得 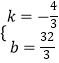
AD所在直线的函数关系式为 ![]()
(2)解:①∵四边形OABC为矩形,
∴BC∥OA,
∴∠DCA=∠CAO,
又∵矩形OABC对折,使A与C重合(折痕为ED),
∴DE为AC的垂直平分线
∴CD=AD,
∴∠DCA=∠DAC,
∴∠DAC=∠CAO,
∴AC平分∠DAO,
∴AC上的点到直线AO和直线AD的距离相等,
∴M点到直线AO和直线AD的距离相等,
∵⊙M始终与x轴相切,
∴M点到直线AO的距离为半径r,
∴M点到直线AD的距离也为半径r,
∴直线AD与⊙M相切;
②⊙M在直线AC上运动,在运动过程中,能与y轴也相切.
如果⊙M与y轴相切,可知圆心M到y轴的距离为半径,
由①可知M(8﹣2r,r)所以只需使8﹣2r=r,
即当r为 ![]() 时,⊙M与x轴、y轴和直线AD都相切,
时,⊙M与x轴、y轴和直线AD都相切,
∴M点的坐标为( ![]() ,
, ![]() )
)
【解析】(1)设CE=t,由于矩形OABC对折,OA=OC=4,从而可知OE=8﹣t,由勾股定理可解得:t的值,由易证CD=CE,从而可求出点D的坐标,利用待定系数法即可求出直线AD的解析式;(2)①由(1)可知:DE是AC的垂直平分线,从而可证明AC平分∠OAD,从而可证明⊙M与直线AD相切;②如果⊙M与y轴相切,可知圆心M到y轴的距离为半径,由①可知M(8﹣2r,r)所以只需使8﹣2r=r,从而可求出r的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学老师布置了一道思考题“计算:(-
 )÷(
)÷(
 )”,小明仔细思考了一番,用了一种不同的方法解决了这个问题.
)”,小明仔细思考了一番,用了一种不同的方法解决了这个问题.小明的解法:原式的倒数为(

 )÷(
)÷( )=(
)=(
 )×(-12)=-4+10=6,所以(-
)×(-12)=-4+10=6,所以(- )÷(
)÷(
 )=
)= .
.(1)请你判断小明的解答是否正确,并说明理由.
(2)请你运用小明的解法解答下面的问题.
计算:(-
 )÷(
)÷(
 +
+ ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】水果店张阿姨以每斤4元的价格购进某种水果若干斤,然后以每斤6元的价格出售,每天可售出150斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出30斤,为保证每天至少售出360斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利450元,张阿姨需将每斤的售价降低多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC=9.6 cm,AB=
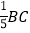 ,CD=2AB,求CD的长.
,CD=2AB,求CD的长.
-
科目: 来源: 题型:
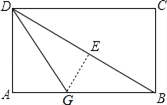
查看答案和解析>>【题目】如图,折叠长方形纸片ABCD,先折出折痕(对角线)BD,在折叠,使AD落在对角线BD上,得折痕DG,若AB=2,BC=1,求AG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆货车从永福超市出发负责送货,向东走了5千米到达小明家,继续向东走了1.5千米到达小红家,然后向西走了9.5千米到达小刚家,最后返回永福超市.
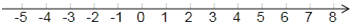
(1)以永福超市为原点,向东为正方向,1个单位长度表示1千米,请你在数轴上标出小明、小红、小刚家的位置.
(2)小明家与小刚家相距多远?
(3)若货车每千米耗油0.6升,那么这辆货车此次送货共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
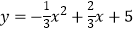 与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C,有一宽度为1的刻度尺沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和点Q,交直线AC于点M和点N,交x轴于点E和点F.
与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C,有一宽度为1的刻度尺沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和点Q,交直线AC于点M和点N,交x轴于点E和点F.
(1)求点A、B、C的坐标;
(2)当点M和点N都在线段AC上时,连接EN,如果点E的坐标为(4,0),求sin∠ANE的值;
(3)在刻度尺平移过程中,当以点P、Q、N、M为顶点的四边形是平行四边形时,求点N的坐标.
相关试题

