【题目】一辆货车从永福超市出发负责送货,向东走了5千米到达小明家,继续向东走了1.5千米到达小红家,然后向西走了9.5千米到达小刚家,最后返回永福超市.
![]()
(1)以永福超市为原点,向东为正方向,1个单位长度表示1千米,请你在数轴上标出小明、小红、小刚家的位置.
(2)小明家与小刚家相距多远?
(3)若货车每千米耗油0.6升,那么这辆货车此次送货共耗油多少升?
参考答案:
【答案】(1)详见解析;(2)小明家与小刚家相距8千米;(3)这辆货车此次送货共耗油11.4升.
【解析】
(1)根据已知,以百货大楼为原点,以向东为正方向,用1个单位长度表示1千米,一辆货车从百货大楼出发,向东走了5千米,到达小明家,继续向东走了1.5千米到达小红家,然后向西走了9.5千米,到达小刚家,最后返回百货大楼,则小明家、小红家和小刚家在数轴上的位置可知;
(2)用小明家的坐标减去小刚家的坐标即可;
(3)这辆货车一共行走的路程,实际上就是5+1.5+9.5+3 (千米),货车从出发到结束行程共耗油量=货车行驶每千米耗油量×货车行驶所走的总路程.
解:(1)如图所示:
![]()
(2)小明家与小刚家相距:5-(-3)=8(千米);
答:小明家与小刚家相距8千米;
(3)这辆货车此次送货共耗油:(5+1.5+9.5+3)×0.6=11.4(升).
答:这辆货车此次送货共耗油11.4升.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC=9.6 cm,AB=
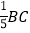 ,CD=2AB,求CD的长.
,CD=2AB,求CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,矩形OABC的边OA、OC分别落在x轴、y轴上,O为坐标原点,且OA=8,OC=4,连接AC,将矩形OABC对折,使点A与点C重合,折痕ED与BC交于点D,交OA于点E,连接AD,如图①.
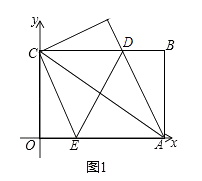
(1)求点D的坐标和AD所在直线的函数关系式;
(2)⊙M的圆心M始终在直线AC上(点A除外),且⊙M始终与x轴相切,如图②.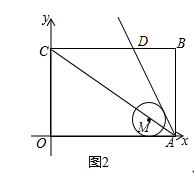
①求证:⊙M与直线AD相切;
②圆心M在直线AC上运动,在运动过程中,能否与y轴也相切?如果能相切,求出此时⊙M与x轴、y轴和直线AD都相切时的圆心M的坐标;如果不能相切,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠长方形纸片ABCD,先折出折痕(对角线)BD,在折叠,使AD落在对角线BD上,得折痕DG,若AB=2,BC=1,求AG.
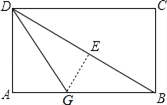
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
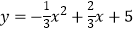 与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C,有一宽度为1的刻度尺沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和点Q,交直线AC于点M和点N,交x轴于点E和点F.
与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C,有一宽度为1的刻度尺沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和点Q,交直线AC于点M和点N,交x轴于点E和点F.
(1)求点A、B、C的坐标;
(2)当点M和点N都在线段AC上时,连接EN,如果点E的坐标为(4,0),求sin∠ANE的值;
(3)在刻度尺平移过程中,当以点P、Q、N、M为顶点的四边形是平行四边形时,求点N的坐标. -
科目: 来源: 题型:
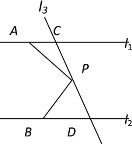
查看答案和解析>>【题目】如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线CD上的一个动点。
(1)如果点P运动到C、D之间时,试探究∠PAC,∠APB,∠PBD之间的关系,并说明理由。
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),∠PAC,∠APB,∠PBD之间 的关系是否发生改变?请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值
(1)(
 -1)
-1)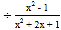 ,其中x的值从不等式
,其中x的值从不等式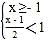 的正整数解中选取.
的正整数解中选取. ÷(a+2-
÷(a+2- ),其中a2+3a-1=0.
),其中a2+3a-1=0.
相关试题

