【题目】A、B两地相距20千米,甲、乙两人都从A地去B地,图中射线l1和l2分别表示甲、乙两人所走路程s(千米)与时间t(小时)之间的关系.
下列说法:
①乙晚出发1小时;
②乙出发3小时后追上甲;
③甲的速度是4千米/小时,乙的速度是6千米/小时;
④乙先到达B地.其中正确的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】C
【解析】
观察函数图象,从图象中获取信息,根据速度,路程,时间三者之间的关系求得结果.
解:由函数图象可知,乙比甲晚出发1小时,故①正确;
乙出发3-1=2小时后追上甲,故②错误;
甲的速度为:12÷3=4(千米/小时),故③正确;
乙的速度为:12÷(3-1)=6(千米/小时),
则甲到达B地用的时间为:20÷4=5(小时),
乙到达B地用的时间为:20÷6=3![]() (小时),
(小时),
1+3![]() =4
=4![]() <5,
<5,
∴乙先到达B地,故④正确;
正确的有3个.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明设计了一个问题,分两步完成:
(1)已知关于x的一元一次方程
 ,请画出数轴,并在数轴上标注a与
,请画出数轴,并在数轴上标注a与 对应的点,分别记作A,B;
对应的点,分别记作A,B;(2)在第1问的条件下,在数轴上另有一点C对应的数为y,C与A的距离是C与B的距离的5倍,且C在表示5的点的左侧,求y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为 __________________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆形纸片⊙O的直径为2,将其沿着两条互相垂直的直径折叠,得到四层的扇形,将最上的一层“撑”开来,“鼓”成一个无底的圆锥,则这个圆锥的高是( )

A.
B.
C.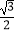
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;
(1)若B、C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC;
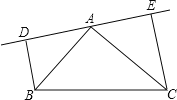
(2)若B、C在DE的两侧(如图所示),其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD内放入六个小正方形后形成一个中心对称图形,其中顶点E、F分别在边BC、AD上,则长AD与宽AB的比值为( )

A.6:5
B.13:10
C.8:7
D.4:3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1…过点A1作y轴的垂线交L2于点A2,过点A2作x轴的垂线交于点A3,过点A3作y轴的垂线交L2于点A4,依次进行下去,则点A2018的坐标为( )
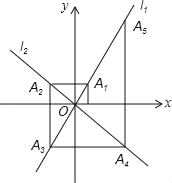
A. (﹣21009,21009) B. (﹣21009,﹣21010)
C. (﹣1009,1009) D. (﹣1009,﹣2018)
相关试题

