【题目】如图,∠1+∠2=180°,∠B=∠D.说明AB∥CD的理由.
补全下面的说理过程,并在括号内填上适当的理由
解:∵∠1+∠2=180°(已知)
∠2=∠AHB( )
∴ (等量代换)
∴DE∥BF( )
∴∠D=∠ ( )
∵∠ =∠B(等量代换)
∴AB∥CD( )

参考答案:
【答案】对顶角相等 ∠1+∠AHB=180° 同旁内角互补,两直线平行 CFH 两直线平行,同位角相等 CFH 内错角相等,两直线平行
【解析】
根据已知条件和对顶角的性质得到∠1+∠AHB=180°根据平行线的判定得到DE∥BF根据平行线的性质得到∠D=∠CFH于是得到结论.
∵∠1+∠2=180°(已知),
∠2=∠AHB(对顶角相等),
∴∠1+∠AHB=180°(等量代换),
∴DE∥BF(同旁内角互补,两直线平行),
∴∠D=∠CFH(两直线平行,同位角相等),
∵∠CFH=∠B(等量代换),
∴AB∥CD(内错角相等,两直线平行).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD是一高为4米的平台,AB是与CD底部相平的一棵树,在平台顶C点测得树顶A点的仰角α=30°,从平台底部向树的方向水平前进3米到达点E,在点E处测得树顶A点的仰角β=60°,求树高AB(结果保留根号)
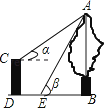
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数y=
 (x>0)的图象交于A(2,﹣1),B(
(x>0)的图象交于A(2,﹣1),B(  ,n)两点,直线y=2与y轴交于点C.
,n)两点,直线y=2与y轴交于点C. 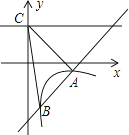
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△APE中,∠PAE=90°,PO是△APE的角平分线,以O为圆心,OA为半径作圆交AE于点G.
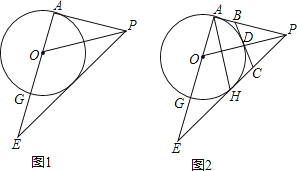
(1)求证:直线PE是⊙O的切线;
(2)在图2中,设PE与⊙O相切于点H,连结AH,点D是⊙O的劣弧 上一点,过点D作⊙O的切线,交PA于点B,交PE于点C,已知△PBC的周长为4,tan∠EAH=
上一点,过点D作⊙O的切线,交PA于点B,交PE于点C,已知△PBC的周长为4,tan∠EAH=  ,求EH的长.
,求EH的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y1=ax2+bx过(﹣2,4),(﹣4,4)两点.
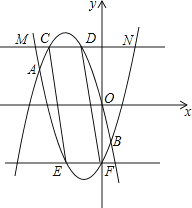
(1)求二次函数y1的解析式;
(2)将y1沿x轴翻折,再向右平移2个单位,得到抛物线y2 , 直线y=m(m>0)交y2于M、N两点,求线段MN的长度(用含m的代数式表示);
(3)在(2)的条件下,y1、y2交于A、B两点,如果直线y=m与y1、y2的图象形成的封闭曲线交于C、D两点(C在左侧),直线y=﹣m与y1、y2的图象形成的封闭曲线交于E、F两点(E在左侧),求证:四边形CEFD是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,延长△ABC的各边,使得BF=AC,AE=CD=AB,连结DE,EF,FD,得到△DEF为等边三角形.
求证:(1)△AEF≌△CDE;
(2)△ABC为等边三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为﹣1和3,则下列结论正确的是( )
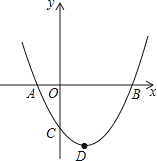
A.2a﹣b=0
B.a+b+c>0
C.3a﹣c=0
D.当a= 时,△ABD是等腰直角三角形
时,△ABD是等腰直角三角形
相关试题

