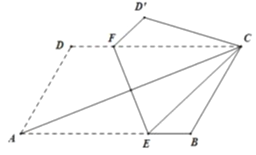
【题目】如图,将平行四边形![]() 沿
沿![]() 对折,使点
对折,使点![]() 落在点
落在点![]() 处,若
处,若![]() ,则
,则![]() 到
到![]() 的距离为____________.
的距离为____________.
参考答案:
【答案】![]()
【解析】分析:过点C作CM⊥AB的延长线于点M,根据翻折的性质,设AE=x,CE=x,BE=6-x,EM=8-x,在△CEM中,利用勾股定理列出方程即可求出x的值.然后算出三角形CBE的面积,根据等面积法即可求出点B到CE的距离.
详解:作CM⊥AB于M,如图所示:
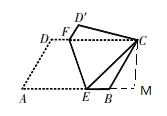
则∠M=90°,
∵四边形ABCD是平行四边形,
∴BC=AD=4,BC∥AD,
∴∠CBM=∠A=60°,
∴∠BCM=30°,
∴BM=![]() BC=4×
BC=4×![]() =2.
=2.
在Rt△BMC中,根据勾股定理可得CM=2![]() .
.
设AE=x,则CE=x,BE=6-x,EM=8-x,
∵CE2=CM2+EM2,
∴x2=(2![]() )2+(8-x)2,
)2+(8-x)2,
解得:x=![]() ,
,
∴CE=![]() ,BE=6-
,BE=6-![]() =
=![]() ,
,
∴S△CBE=![]() .
.
∴点B到CE的距离= S△CBE÷CE×2=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图A在数轴上所对应的数为﹣2.
(1)点B在点A右边距A点4个单位长度,求点B所对应的数;
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点 B 以每秒2个单位长度沿数轴向右运动,当点A运动到﹣6所在的点处时,求A,B两点间距离.
(3)在(2)的条件下,现A点静止不动,B点再以每秒2个单位长度沿数轴向左运动时,经过多长时间A,B两点相距4个单位长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
 的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).
的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1). 
(1)求反比例函数与一次函数的表达式;
(2)点E为y轴上一个动点,若S△AEB=10,求点E的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AD=
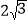 ,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为____________.
,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为____________.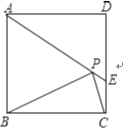
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上两点A、B对应的数分别为-1、3, 点P是数轴上一动点P

(1)(4分)若点P到点A,点B的距离相等,求点P对应的数;
(2) (6分)当点P以每分钟5个单位长度的速度从O点向右运动时,点A以每分钟3个单位长度的速度向右运动,点B以每分钟2个单位长度的速度向右运动,问几分钟时点P到点A,点B的距离相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校开展学生安全知识竞赛.现抽取部分学生的竞赛成绩(满分为100分,得分均为整数)进行统计,绘制了图中两幅不完整的统计图.根据图中信息,回答下列问题:
(1)a= ,n= ;
(2)补全频数分布直方图;
(3)该校共有2000名学生.若成绩在80分以上的为优秀,请你估计该校成绩优秀的学生人数.
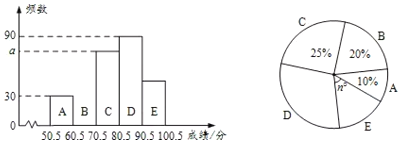
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算结果为正数的是( )
A.(﹣ )﹣2
)﹣2
B.﹣(﹣ )0
)0
C.(﹣ )3
)3
D.﹣| |
|
相关试题

