【题目】在平面直角坐标系xOy中,对称轴为直线x=1的抛物线y=ax2+bx+8过点(﹣2,0).
(1)求抛物线的表达式,并写出其顶点坐标;
(2)现将此抛物线沿y轴方向平移若干个单位,所得抛物线的顶点为D,与y轴的交点为B,与x轴负半轴交于点A,过B作x轴的平行线交所得抛物线于点C,若AC∥BD,试求平移后所得抛物线的表达式.
参考答案:
【答案】(1)y=﹣x2+2x+8,其顶点为(1,9)(2)y=﹣x2+2x+3
【解析】试题分析:(1)根据对称轴为直线x=1的抛物线y=ax2+bx+8过点(﹣2,0),可得 ,解得
,解得![]() 即可求解,(2)设令平移后抛物线为
即可求解,(2)设令平移后抛物线为![]() ,
,
可得D(1,k),B(0,k-1),且![]() ,根据BC平行于x轴,可得点C与点B关于对称轴x=1对称,可得C(2,k-1), 根据
,根据BC平行于x轴,可得点C与点B关于对称轴x=1对称,可得C(2,k-1), 根据![]() ,解得
,解得![]() ,即
,即![]() .
.
作DH⊥BC于H,CT⊥x轴于T, 则在△DBH中,HB=HD=1,∠DHB=90°,
又AC∥BD,得△CTA∽△DHB,所以CT=AT,即![]() ,
,
解得k=4,即可求平移后的二次函数解析式.
试题解析:(1)由题意得: 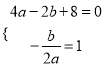 ,解得:
,解得: ![]() ,
,
所以抛物线的表达式为![]() ,其顶点为(1,9).
,其顶点为(1,9).
(2)令平移后抛物线为![]() ,
,
易得D(1,k),B(0,k-1),且![]() ,
,
由BC平行于x轴,知点C与点B关于对称轴x=1对称,得C(2,k-1),
由![]() ,解得
,解得![]() (舍正),即
(舍正),即![]() .
.
作DH⊥BC于H,CT⊥x轴于T,
则在△DBH中,HB=HD=1,∠DHB=90°,
又AC∥BD,得△CTA∽△DHB,
所以CT=AT,即![]() ,
,
解得k=4,
所以平移后抛物线表达式为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图象(折线OEFPMN)描述了某汽车在行驶过程中速度与时间的函数关系,下列说法中错误的是( )

A. 第3分时汽车的速度是40千米/时
B. 第12分时汽车的速度是0千米/时
C. 从第3分到第6分,汽车行驶了120千米
D. 从第9分到第12分,汽车的速度从60千米/时减少到0千米/时
-
科目: 来源: 题型:
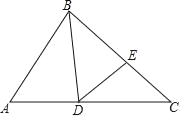
查看答案和解析>>【题目】如图,BD是△ABC的角平分线,点E位于边BC上,已知BD是BA与BE的比例中项.
(1)求证:∠CDE=
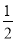 ∠ABC;
∠ABC;(2)求证:ADCD=ABCE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把Rt△ABC绕顶点C顺时针旋转90°得到Rt△DFC,若直线DF垂直平分AB,垂足为点E,连接BF,CE,且BC=2.下面四个结论:

①BF=
 ;
;②∠CBF=45°;
③∠CED=30°;
④△ECD的面积为
 ,
,其中正确的结论有_____.(填番号)
-
科目: 来源: 题型:
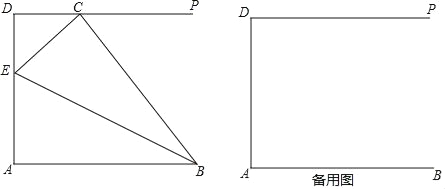
查看答案和解析>>【题目】如图,线段AB=5,AD=4,∠A=90°,DP∥AB,点C为射线DP上一点,BE平分∠ABC交线段AD于点E(不与端点A、D重合).
(1)当∠ABC为锐角,且tan∠ABC=2时,求四边形ABCD的面积;
(2)当△ABE与△BCE相似时,求线段CD的长;
(3)设CD=x,DE=y,求y关于x的函数关系式,并写出定义域.
-
科目: 来源: 题型:
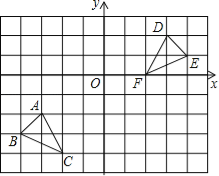
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC和△DEF的顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
(1)画出△ABC向上平移4个单位长度后所得到的△A1B1C1;
(2)画出△DEF绕点O按顺时针方向旋转90°后所得到的△D1E1F1;
(3)△A1B1C1和△D1E1F1组成的图形是轴对称图形吗?如果是,请直接写出对称轴所在直线的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2016个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D…的规律绕在ABCD的边上,则细线另一端所在位置的点的坐标是( )
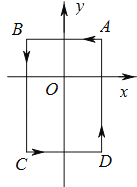
A. (0,-2) B. (-1,-1) C. (-1,0) D. (1,-2)
相关试题

