【题目】如图,AC 平分∠BAD,过 C 点作 CE⊥AB 于 E,并且 2AE=AB+AD,则下列结论:
①AB=AD+2BE;②∠DAB+∠DCB=180°;③CD=CB;④S△ABC=S△ACD+S△BCE,其中不正确的结论个数有( )

A. 0 B. 1 C. 2 D. 3
参考答案:
【答案】B
【解析】
过C作CF⊥AD于F.先判定Rt△ACF≌Rt△ACE,即可得出BE=DF,再判定△CDF≌△CBE,即可得到CD=CB;再根据四边形内角和以及三角形的面积计算公式,即可得到正确结论.
如图,过C作CF⊥AD于F.
∵AC平分∠BAD,CE⊥AB,CF⊥AD,∴CF=CE,∴Rt△ACF≌Rt△ACE(HL),∴AF=AE,∴AB+AD=(AE+BE)+(AF﹣DF)=2AE+BE﹣DF.
又∵AB+AD=2AE,∴BE=DF,∴AB﹣AD=(AE+BE)﹣(AF﹣DF)=BE+DF=2BE,即AB=AD+2BE,故①正确;
∵BE=DF,∠CEB=∠F=90°,CF=CE,∴△CDF≌△CBE(SAS),∴∠B=∠CDF,CD=CB,故③正确;
又∵∠ADC+∠CDF=180°,∴∠ADC+∠B=180°,∴四边形ABCD中,∠DAB+∠BCD=360°﹣180°=180°,故②正确;
∵AB=AD+2BE,CE=CF,∴由等式性质可得:![]() AB×CE
AB×CE![]() AD×CF+2
AD×CF+2![]() BE×CE,即S△ABC=S△ACD+2S△BCE,故④错误.
BE×CE,即S△ABC=S△ACD+2S△BCE,故④错误.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,已知⊙O的半径为1,菱形ABCD的三个顶点A、B、D在⊙O上,且CD与⊙O相切.
(1)求证:BC与⊙O相切;
(2)求阴影部分面积.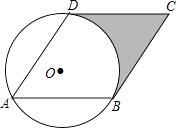
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)先化简,再求值
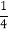 x2+2(x-
x2+2(x- y2)-
y2)- (-3x2+2y2)-
(-3x2+2y2)- x,其中x=2,y=-3;
x,其中x=2,y=-3;(2)已知A=2a2-a,B=-5a+1.
①化简:3A-2B+2;
②当a=-
 时,求3A-2B+2的值.
时,求3A-2B+2的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在线段AB的延长线上,AC=
 BC,D在AB的反向延长线上,BD=
BC,D在AB的反向延长线上,BD=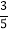 DC.
DC.(1)在图上画出点C和点D的位置;
(2)设线段AB长为x,则BC=__ __,AD=__ __;(用含x的代数式表示)
(3)设AB=12 cm,求线段CD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC 三边的中线 AD,BE,CF 相交于点 G,若 S△ABC=15,则图中阴影部分面积是______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,A(2018,0),B(0,2014),以 AB 为斜边作等腰Rt△ABC,则 C点坐标为__________
-
科目: 来源: 题型:
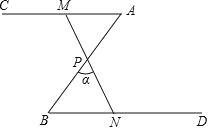
查看答案和解析>>【题目】如图,∠A=∠B=50°,P 为 AB 中点,点 M 为射线 AC 上(不与点 A 重合)的任意点,连接 MP,并使 MP 的延长线交射线 BD 于点 N,设∠ BPN=α.
(1)求证:△APM≌△BPN;
(2)当 MN=2BN 时,求α的度数;
相关试题

