【题目】在△ABC中,∠BAC=100°,∠ABC=∠ACB,点D在直线BC上运动(不与点B、C重合),点E在射线AC上运动,且∠ADE=∠AED,设∠DAC=n.
(1)如图(1),当点D在边BC上时,且n=36°,则∠BAD= _________,∠CDE= _________.
(2)如图(2),当点D运动到点B的左侧时,其他条件不变,请猜想∠BAD和∠CDE的数量关系,并说明理由.
(3)当点D运动到点C的右侧时,其他条件不变,∠BAD和∠CDE还满足(2)中的数量关系吗?请画出图形,并说明理由.

参考答案:
【答案】64° 32°
【解析】
(1)由∠BAC=100°,可求出∠ABC=∠ACB=40°,当∠DAC=36°时,根据∠BAD=∠BAC-∠DAC可求出∠BAD的度数,根据等腰三角形的性质求出∠ADE=∠AED的度数,再根据三角形的外角的性质求解.
(2) 由思路(1)可知∠ABC=∠ACB=40°,以及∠ADE=∠AED=![]() ,∠CDE=∠ACB-∠AED,∠BAD=n-100°,即可求解.
,∠CDE=∠ACB-∠AED,∠BAD=n-100°,即可求解.
(3)根据(1)的思路,可知∠ABC=∠ACB=40°,∠ADE=∠AED=![]() ,∠CDE=∠ACD-∠AED,∠BAD=100°+n,即可求解.
,∠CDE=∠ACD-∠AED,∠BAD=100°+n,即可求解.
(1)∠BAD=∠BAC-∠DAC=100°-36°=64°.
∵在△ABC中,∠BAC=100°,∠ABC=∠ACB,
∴∠ABC=∠ACB=40°,
∴∠ADC=∠ABC+∠BAD=40°+64°=104°.
∵∠DAC=36°,∠ADE=∠AED,
∴∠ADE=∠AED=72°,
∴∠CDE=∠ADC-∠ADE=104°-72°=32°.
故答案为64°,32°.
(2)∠BAD=2∠CDE,理由如下:
如图(2),在△ABC中,∠BAC=100°,
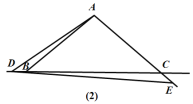
∴∠ABC=∠ACB=40°.
在△ADE中,∠DAC=n,
∴∠ADE=∠AED=![]() .
.
∵∠ACB=∠CDE+∠AED,
∴∠CDE=∠ACB-∠AED=40°-![]() =
=![]() .
.
∵∠BAC=100°,∠DAC=n,
∴∠BAD=n-100°,
∴∠BAD=2∠CDE;
(3)∠BAD=2∠CDE,理由如下:
如图(3),在△ABC中,∠BAC=100°,
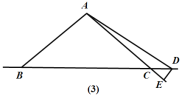
∴∠ABC=∠ACB=40°,
∴∠ACD=140°.
在△ADE中,∠DAC=n,
∴∠ADE=∠AED=![]() .
.
∵∠ACD=∠CDE+∠AED,
∴∠CDE=∠ACD-∠AED=140°-![]() =
=![]() .
.
∵∠BAC=100°,∠DAC=n,
∴∠BAD=100°+n,
∴∠BAD=2∠CDE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在锐角
 中,
中, 是
是 边上的高.
边上的高.  ,且
,且
 .连接
.连接 ,交
,交 的延长线于点
的延长线于点 ,连接
,连接 .下列结论:①
.下列结论:① ;②
;② ;③
;③ ;④
;④ .其中一定正确的个数是( )
.其中一定正确的个数是( )
A.
 个B.
个B. 个
个C.
 个D.
个D. 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的方格纸中,小正方形的顶点叫做格点,
 是一个格点三角形(即
是一个格点三角形(即 的三个顶点都在格点上),根据要求回答下列问题:
的三个顶点都在格点上),根据要求回答下列问题: 画出
画出 先向左平移6格,再向上平移
先向左平移6格,再向上平移 格所得的
格所得的 ;
; 利用网格画出
利用网格画出 中
中 边上的高
边上的高 .
. 过点
过点 画直线,将
画直线,将 分成面积相等的两个三角形;
分成面积相等的两个三角形; 画出与
画出与 有一条公共边,且与
有一条公共边,且与 全等的格点三角形.
全等的格点三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学计划购进若干个甲种规格的排球和乙种规格的足球.如果购买
 个甲种规格的排球和
个甲种规格的排球和 个乙种规格的足球,一共需要花费
个乙种规格的足球,一共需要花费 元;如果购买
元;如果购买 个甲种规格的排球和
个甲种规格的排球和 个乙种规格的足球,一共需要花费
个乙种规格的足球,一共需要花费 元.
元. 求每个甲种规格的排球和每个乙种规格的足球的价格分别是多少元?
求每个甲种规格的排球和每个乙种规格的足球的价格分别是多少元? 如果学校要购买甲种规格的排球和乙种规格的足球共
如果学校要购买甲种规格的排球和乙种规格的足球共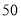 个,并且预算总费用不超过3080元,那么该学校至多能购买多少个乙种规格的足球?
个,并且预算总费用不超过3080元,那么该学校至多能购买多少个乙种规格的足球? -
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级学生全部参加“初二生物地理会考”,从中抽取了部分学生的生物考试成绩,将他们的成绩进行统计后分为A,B,C,D四等,并将统计结果绘制成如下的统计图,请结合图中所给的信息解答下列问题
(1)抽取了______名学生成绩;(2)请把条形统计图补充完整;
(3)扇形统计图中等级D所在的扇形的圆心角度数是______;
(4)若A,B,C代表合格,该校初二年级有300名学生,求全年级生物合格的学生共约多少人

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,□ABCD中,BE平分∠ABC且交边AD于点E,如果AB=6cm,BC=10cm,
试求:⑴□ABCD的周长;⑵线段DE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 是∠
是∠ 内的一点,过点
内的一点,过点 作
作 于点
于点 于点
于点 ,且
,且 .
. 求证:
求证:  ;
;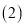 如图②,点
如图②,点 是射线
是射线 上一点,点
上一点,点 是线段
是线段 上一点,且
上一点,且 ,若
,若 .求线段
.求线段 的长.
的长. 如图③,若
如图③,若 ,将
,将 绕点
绕点 以每秒
以每秒 的速度顺时针旋转,
的速度顺时针旋转, 秒后,
秒后,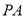 开始绕点
开始绕点 以每秒
以每秒 的速度顺时针旋转,
的速度顺时针旋转,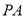 旋转
旋转 后停止,此时
后停止,此时 也随之停止旋转。旋转过程中,
也随之停止旋转。旋转过程中,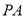 所在直线与
所在直线与 所在直线的交点记为
所在直线的交点记为 所在直线与
所在直线与 所在直线的交点记为
所在直线的交点记为 .问
.问 旋转几秒时,
旋转几秒时, ?
?
相关试题

