【题目】如图,在锐角![]() 中,
中,![]() 是
是![]() 边上的高.
边上的高. ![]() ,且
,且![]()
![]() .连接
.连接![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中一定正确的个数是( )
.其中一定正确的个数是( )

A.![]() 个B.
个B.![]() 个
个
C.![]() 个D.
个D.![]() 个
个
参考答案:
【答案】A
【解析】
首先根据题意,可得出∠FAE+∠BAD=90°,∠GAE+∠CAD=90°,进而得出∠FAE+∠BAD+∠GAE+∠CAD=180°,可判定①结论正确;由∠BAF+∠BAC=∠CAG+∠BAC,![]() ,得出∠FAC=∠BAG,
,得出∠FAC=∠BAG,![]()
![]() ,判定△FAC≌△BAG,判定②结论正确;由∠EAF+∠BAD=90°,∠BAD+∠ABC=90°,得出∠EAF=∠ABC,可判定④结论正确;由∠AFC=∠ABG,∠AFC+∠FHA=90°,对顶角相等,得出∠ABG+∠BHC=90°,即可判定③结论正确;故正确的结论有4个.
,判定△FAC≌△BAG,判定②结论正确;由∠EAF+∠BAD=90°,∠BAD+∠ABC=90°,得出∠EAF=∠ABC,可判定④结论正确;由∠AFC=∠ABG,∠AFC+∠FHA=90°,对顶角相等,得出∠ABG+∠BHC=90°,即可判定③结论正确;故正确的结论有4个.
解:∵![]() 是
是![]() 边上的高.
边上的高. ![]() ,
,
∴∠FAE+∠BAD=90°,∠GAE+∠CAD=90°
∴∠FAE+∠BAD+∠GAE+∠CAD=180°
∴![]() ,①结论正确;
,①结论正确;
∵![]()
∴∠BAF+∠BAC=∠CAG+∠BAC
∴∠FAC=∠BAG
又∵![]()
![]()
∴△FAC≌△BAG(SAS)
∴BG=CF,②结论正确;
∵∠EAF+∠BAD=90°,∠BAD+∠ABC=90°
∴∠EAF=∠ABC,④结论正确;
令CF和AB、BG分别交于点H、I
∵△FAC≌△BAG
∴∠AFC=∠ABG
又∵∠AFC+∠FHA=90°,∠FHA=∠BHC(对顶角相等)
∴∠ABG+∠BHC=90°,即∠BIF=90°,即![]() ,
,
③结论正确;正确的个数有4个.
故选:A.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AE=AB,直线DE交BC于点F,则∠BEF=( )

A. 50°B. 30°C. 60°D. 45°
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点(x1,y1),(x2,y2),(x3,y3)都是反比例函数y=﹣
 图象上的点,并且y1<0<y2<y3,则下列各式中正确的是( )
图象上的点,并且y1<0<y2<y3,则下列各式中正确的是( )A.x1<x2<x3 B.x1<x3<x2
C.x2<x1<x3 D.x2<x3<x1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点E,F分别在边BC,CD上,如果AE=4,EF=3,AF=5,那么正方形ABCD的面积等于_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的方格纸中,小正方形的顶点叫做格点,
 是一个格点三角形(即
是一个格点三角形(即 的三个顶点都在格点上),根据要求回答下列问题:
的三个顶点都在格点上),根据要求回答下列问题: 画出
画出 先向左平移6格,再向上平移
先向左平移6格,再向上平移 格所得的
格所得的 ;
; 利用网格画出
利用网格画出 中
中 边上的高
边上的高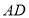 .
. 过点
过点 画直线,将
画直线,将 分成面积相等的两个三角形;
分成面积相等的两个三角形; 画出与
画出与 有一条公共边,且与
有一条公共边,且与 全等的格点三角形.
全等的格点三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学计划购进若干个甲种规格的排球和乙种规格的足球.如果购买
 个甲种规格的排球和
个甲种规格的排球和 个乙种规格的足球,一共需要花费
个乙种规格的足球,一共需要花费 元;如果购买
元;如果购买 个甲种规格的排球和
个甲种规格的排球和 个乙种规格的足球,一共需要花费
个乙种规格的足球,一共需要花费 元.
元. 求每个甲种规格的排球和每个乙种规格的足球的价格分别是多少元?
求每个甲种规格的排球和每个乙种规格的足球的价格分别是多少元? 如果学校要购买甲种规格的排球和乙种规格的足球共
如果学校要购买甲种规格的排球和乙种规格的足球共 个,并且预算总费用不超过3080元,那么该学校至多能购买多少个乙种规格的足球?
个,并且预算总费用不超过3080元,那么该学校至多能购买多少个乙种规格的足球? -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠BAC=100°,∠ABC=∠ACB,点D在直线BC上运动(不与点B、C重合),点E在射线AC上运动,且∠ADE=∠AED,设∠DAC=n.
(1)如图(1),当点D在边BC上时,且n=36°,则∠BAD= _________,∠CDE= _________.
(2)如图(2),当点D运动到点B的左侧时,其他条件不变,请猜想∠BAD和∠CDE的数量关系,并说明理由.
(3)当点D运动到点C的右侧时,其他条件不变,∠BAD和∠CDE还满足(2)中的数量关系吗?请画出图形,并说明理由.

相关试题

