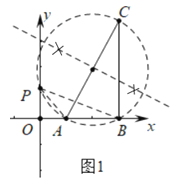
【题目】已知A(2,0),B(6,0),CB⊥x轴于点B,连接AC
画图操作:
(1)在y正半轴上求作点P,使得∠APB=∠ACB(尺规作图,保留作图痕迹)

理解应用:
(2)在(1)的条件下,
①若tan∠APB ![]() ,求点P的坐标
,求点P的坐标
②当点P的坐标为 时,∠APB最大
拓展延伸:
(3)若在直线y![]() x+4上存在点P,使得∠APB最大,求点P的坐标
x+4上存在点P,使得∠APB最大,求点P的坐标

参考答案:
【答案】(1)图形见解析(2)(0,2),(0,4)(0,2![]() )(3)(
)(3)(![]() ,
,![]() )
)
【解析】试题分析:(1)以AC为直径画圆交y轴于P,连接PA、PB,∠PAB即为所求;
(2)①由题意AC的中点K(4,4),以K为圆心AK为半径画圆,交y轴于P和P′,易知P(0,2),P′(0,6);
②当⊙K与y轴相切时,∠APB的值最大,(3)如图3中,当经过AB的园与直线相切时,∠APB最大.想办法求出点P坐标即可解决问题;
试题解析:解:(1)∠APB如图所示;
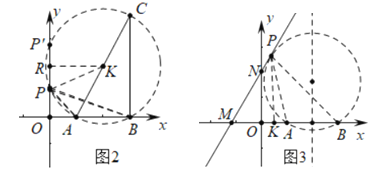
(2)①如图2中,∵∠APB=∠ACB,∴tan∠ACB=tan∠APB=![]() =
=![]() .∵A(2,0),B(6,0),∴AB=4,BC=8,∴C(6,8),∴AC的中点K(4,4),以K为圆心AK为半径画圆,交y轴于P和P′,易知P(0,2),P′(0,6).
.∵A(2,0),B(6,0),∴AB=4,BC=8,∴C(6,8),∴AC的中点K(4,4),以K为圆心AK为半径画圆,交y轴于P和P′,易知P(0,2),P′(0,6).
②当⊙K与y轴相切时,∠APB的值最大,此时AK=PK=4,AC=8,∴BC=![]() =4
=4![]() ,∴C(6,4
,∴C(6,4![]() ),∴K(4,2
),∴K(4,2![]() ),∴P(0,2
),∴P(0,2![]() ).故答案为:(0,2
).故答案为:(0,2![]() ).
).
(3)如图3中,当经过AB的园与直线相切时,∠APB最大.∵直线y=![]() x+4交x轴于M(﹣3,0),交y轴于N(0,4).∵MP是切线,∴MP2=MAMB,∴MP=3
x+4交x轴于M(﹣3,0),交y轴于N(0,4).∵MP是切线,∴MP2=MAMB,∴MP=3![]() ,作PK⊥OA于K.∵ON∥PK,∴
,作PK⊥OA于K.∵ON∥PK,∴![]() =
=![]() =
=![]() ,∴
,∴![]() =
=![]() =
=![]() ,∴PK=
,∴PK=![]() ,MK=
,MK=![]() ,∴OK=
,∴OK=![]() ﹣3,∴P(
﹣3,∴P(![]() ﹣3,
﹣3,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】重庆市的重大惠民工程﹣﹣公租房建设已陆续竣工,计划10年内解决低收入人群的住房问题,前6年,每年竣工投入使用的公租房面积y(单位:百万平方米),与时间x的关系是y=
 x+5,(x单位:年,1≤x≤6且x为整数);后4年,每年竣工投入使用的公租房面积y(单位:百万平方米),与时间x的关系是y=-
x+5,(x单位:年,1≤x≤6且x为整数);后4年,每年竣工投入使用的公租房面积y(单位:百万平方米),与时间x的关系是y=- x+
x+ (x单位:年,7≤x≤10且x为整数).假设每年的公租房全部出租完.另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金z(单位:元/m2)与时间x(单位:年,1≤x≤10且x为整数)满足一次函数关系如下表:
(x单位:年,7≤x≤10且x为整数).假设每年的公租房全部出租完.另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金z(单位:元/m2)与时间x(单位:年,1≤x≤10且x为整数)满足一次函数关系如下表:z(元/m2)
50
52
54
56
58
…
x(年)
1
2
3
4
5
…
(1)求出z与x的函数关系式;
(2)求政府在第几年投入的公租房收取的租金最多,最多为多少百万元;
(3)若第6年竣工投入使用的公租房可解决20万人的住房问题,政府计划在第10年投入的公租房总面积不变的情况下,要让人均住房面积比第6年人均住房面积提高a%,这样可解决住房的人数将比第6年减少1.35a%,求a的值.
(参考数据:
 ,
, ,
, )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】某市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如下表(单位:环):

根据表格中的数据,可计算出甲、乙两人的平均成绩都是9(环).
(1)分别计算甲、乙六次测试成绩的方差;
(2)根据数据分析的知识,你认为选 名队员参赛.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把四张大小相同的长方形卡片(如图①)按图②、图③两种放法放在一个底面为长方形(长比宽多
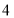 )的盒底上,底面为被卡片覆盖的部分用阴影表示,若记图②中阴影部分的周长为
)的盒底上,底面为被卡片覆盖的部分用阴影表示,若记图②中阴影部分的周长为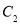 ,图③中阴影部分的周长为
,图③中阴影部分的周长为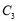 ,则
,则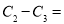 ________.
________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:我们知道,
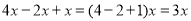 ,类似地,我们把
,类似地,我们把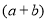 看成一个整体,则
看成一个整体,则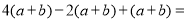
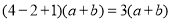 .“整体思想”是中学教学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.
.“整体思想”是中学教学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.尝试应用:
(1)把
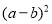 看成一个整体,合并
看成一个整体,合并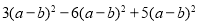 的结果是______________.
的结果是______________.(2)当
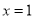 时,代数式
时,代数式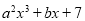 的值为
的值为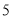 ,则当
,则当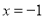 时,求代数式
时,求代数式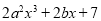 的值.
的值.拓广探索:
(3)已知
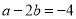 ,
,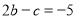 ,
,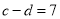 ,求
,求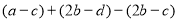 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某运输部门规定:办理托运,当一件物品的重量不超过
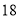 千克时,需付基础费
千克时,需付基础费 元和保险费
元和保险费 元;为了限制过重物品的托运,当一件物品的重量超过
元;为了限制过重物品的托运,当一件物品的重量超过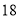 千克时,除了付以上基础费和保险费外,超过部分每千克还需付
千克时,除了付以上基础费和保险费外,超过部分每千克还需付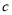 元的超重费.设某件物品的重量为
元的超重费.设某件物品的重量为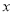 千克,支付费用为
千克,支付费用为 元.
元.(1)当
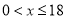 时,
时, ______________(用式子表示);
______________(用式子表示);当
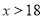 时,
时, ______________(用式子表示);
______________(用式子表示);(2)甲、乙、丙三人各托运一件物品,物品的重量与支付费用如下表所示:
托运人
物品重量/千克
支付费用/元
甲
14
33
乙
20
39
丙
30
根据以上提供的信息确定
 的值,并计算出丙所支付的费用
的值,并计算出丙所支付的费用 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】工厂接到订单,需要边长为(a+3)和3的两种正方形卡纸.
(1)仓库只有边长为(a+3)的正方形卡纸,现决定将部分边长为(a+3)的正方形纸片,按图甲所示裁剪得边长为3的正方形.
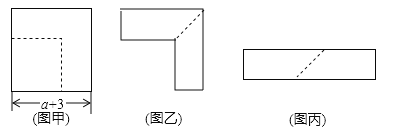
①如图乙,求裁剪正方形后剩余部分的面积(用含a代数式来表示);
②剩余部分沿虚线又剪拼成一个如图丙所示长方形(不重叠无缝隙),则拼成的长方形的边长多少?(用含a代数式来表示);
(2)若将裁得正方形与原有正方形卡纸放入长方体盒子底部,按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),盒子底部中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2测得盒子底部长方形长比宽多3,则S2﹣S1的值为 .

相关试题

