【题目】【感受联系】在初二的数学学习中,我们感受过等腰三角形与直角三角形的密切联系.等腰三角形作底边上的高线可转化为直角三角形,直角三角形沿直角边翻折可得到等腰三角形等等.
(1)【探究发现】某同学运用这一联系,发现了“30°角所对的直角边等于斜边的一半”.并给出了如下的部分探究过程,请你补充完整证明过程
已知:如图,
在 ![]() △
△![]() 中,
中, ![]() °,
°, ![]() °.
°.
求证: ![]() .
.
(2)【灵活运用】该同学家有一张折叠方桌如图①所示,方桌的主视图如图②.经测得 ![]() ,
, ![]() ,将桌子放平,两条桌腿叉开的角度
,将桌子放平,两条桌腿叉开的角度 ![]() .
.
求:桌面与地面的高度.
参考答案:
【答案】
(1)证明:取AB的中点D,连接CD,
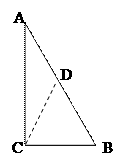
∵在Rt△ABC中,点D是AB的中点,
∴CD=DB= ![]() AB ,
AB ,
∵∠C=90°,∠A=30°,
∴∠B=60°,
∴△DBC是等边三角形 ,
∴BC=CD=DB,
∴BC= ![]() AB
AB
(2)解:过O作,OE⊥AB于E,OF⊥CD于点F,
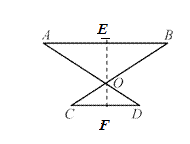
∵OA=OB,∠AOB=120°,
∴∠A=30° ,
在Rt△AOE中,OA=90,∠A=30°, ![]() ,
,
∴OE=45 ,
同理:OF=15.
所以,桌面与地面的高度是60cm.
【解析】(1)根据在直角三角形中,斜边上的中线是斜边的一半;得到CD=DB=![]() AB;根据三角形内角和定理求出∠B=60°,得到△DBC是等边三角形 ,得到BC=CD=DB,得到BC=
AB;根据三角形内角和定理求出∠B=60°,得到△DBC是等边三角形 ,得到BC=CD=DB,得到BC=![]() AB;(2)根据等腰三角形的性质,得到∠A=30° ,根据在直角三角形中,30度角所对的边是斜边的一半;得到OE=
AB;(2)根据等腰三角形的性质,得到∠A=30° ,根据在直角三角形中,30度角所对的边是斜边的一半;得到OE=![]() OB,同理OF=
OB,同理OF=![]() OC,求出桌面与地面的高度.
OC,求出桌面与地面的高度.
【考点精析】解答此题的关键在于理解含30度角的直角三角形的相关知识,掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半,以及对直角三角形斜边上的中线的理解,了解直角三角形斜边上的中线等于斜边的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
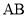 与
与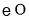 相切于点
相切于点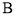 ,
,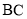 为
为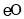 的弦,
的弦,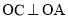 ,
,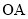 与
与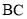 相交于点
相交于点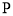 ;
;(1)求证:
 ;
;(2)若
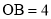 ,
,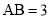 ,求线段
,求线段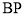 的长.
的长.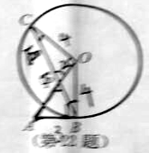
-
科目: 来源: 题型:
查看答案和解析>>【题目】钓鱼诸岛是中国的固有领土,位于中国东海,面积约6344000平方米,数据6344000用科学记数法表示为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】桌面上有四张正面分别标有数字
 ,
,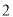 ,
,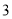 ,
,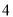 的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上洗匀.
的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上洗匀.(1)随机翻开一张卡片,正面所标数字大于
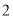 的概率为 ;
的概率为 ;(2)随机翻开一张卡片,从余下的三张卡片中再翻开一张,求翻开的两张卡片正面所标数字之和是偶数的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知在长方形ABCD中, AD=8, AB=4,将长方形ABCD沿着对角线BD折叠,使点C落在
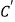 处,
处, 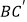 交AD于点E.
交AD于点E.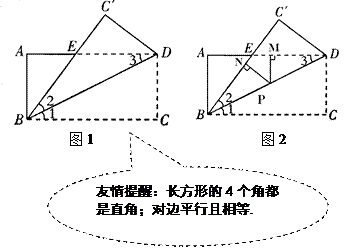
(1)求证:△BED是等腰三角形.
(2)求DE的长.
(3)如图2,若点P是BD上一动点,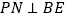 于点N,
于点N, 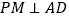 于点M,问: PN+PM的长是否为定值?如果是,请求出该值,如果不是,请说明理由.
于点M,问: PN+PM的长是否为定值?如果是,请求出该值,如果不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a3a2=a6
B.(a2b)3=a6b3
C.a8÷a2=a4
D.a+a=a2 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,直线
 交x轴、y轴分别于点A、点B,将△AOB绕坐标原点逆时针旋转
交x轴、y轴分别于点A、点B,将△AOB绕坐标原点逆时针旋转  得到△COD.直线CD交直线AB于点E,如图1.
得到△COD.直线CD交直线AB于点E,如图1.
图1
(1)求:直线CD的函数关系式.
(2)如图2,连接OE,过点O作 交直线CD于点F,如图2.
交直线CD于点F,如图2.
图2
① 求证: =
=  .
.
② 求:点F的坐标.
(3)若点P是直线DC上一点,点Q是x轴上一点(点Q不与点O重合),当△DPQ和△DOC全等时,直接写出点P的坐标.
相关试题

