【题目】在平面直角坐标系中,直线 ![]() 交x轴、y轴分别于点A、点B,将△AOB绕坐标原点逆时针旋转
交x轴、y轴分别于点A、点B,将△AOB绕坐标原点逆时针旋转 ![]() 得到△COD.直线CD交直线AB于点E,如图1.
得到△COD.直线CD交直线AB于点E,如图1.
图1
(1)求:直线CD的函数关系式.
(2)如图2,连接OE,过点O作 ![]() 交直线CD于点F,如图2.
交直线CD于点F,如图2.
图2
① 求证: ![]() =
= ![]() .
.
② 求:点F的坐标.
(3)若点P是直线DC上一点,点Q是x轴上一点(点Q不与点O重合),当△DPQ和△DOC全等时,直接写出点P的坐标.
参考答案:
【答案】
(1)解: ![]() ,
,
令x=0,B(0,4),令y=0,A(3,0),则D(-4,0),C(0, ![]()
解设过D,C直线解析式是 ![]() ,
,
![]() ,
,
解得  ,
,
![]()
(2)解:① ![]() ,
,
![]()
![]() ,
,
△AOB旋转了90°,所以 ![]() ,
, ![]() ,
,
 ,
,
![]() △DFO≌△BOE,可得OF=OE ,
△DFO≌△BOE,可得OF=OE ,
![]() ∠OEF=45°.
∠OEF=45°.
②联立  ,解得E(
,解得E( ![]() ,由①知,△DFO≌△BOE,
,由①知,△DFO≌△BOE,
所以旋转以后得F ( ![]() ).
).
(3)解:如图,

与 ![]() CDO面积相等(也就是全等)满足题意的三角形有三个,
CDO面积相等(也就是全等)满足题意的三角形有三个,
在△![]() ,,D(-4,0)点是C(0,3)和
,,D(-4,0)点是C(0,3)和 ![]() 中点,
中点, ![]() ,
, ![]() ,
,
所以有 ![]() ,
,
在![]() ,由题意知Q3,(1,0),OD=O
,由题意知Q3,(1,0),OD=O ![]() ,勾股定理知,P3纵坐标
,勾股定理知,P3纵坐标 ![]() ,代入直线
,代入直线 ![]() ,得到P3(
,得到P3( ![]() ))
))
在![]() 由题意知D(-4,0)是P1(x,y),P3(
由题意知D(-4,0)是P1(x,y),P3( ![]() )中点,
)中点, ![]() =-4,
=-4, ![]() =0,
=0,  ,
,
所以 ![]() ,
,
所以P的坐标是, ![]() ,
, ![]() ,
, ![]() .
.
【解析】(1)根据题意得到A、B两点的坐标,由旋转的性质,得到C、D的坐标,求出直线CD的函数关系式;(2)根据角的和差和旋转的性质,得到△DFO≌△BOE,得到OF=OE,由OF⊥OE ,得到∠OEF=45°;联立两条直线,得到得到点E的坐标,由△DFO≌△BOE和旋转的性质,得到点F的坐标;(3)根据题意得到与△CDO面积相等(也就是全等)满足题意的三角形有三个,在△DP2Q2 中,得到D、C的坐标,求出P点坐标;在△DP3Q3中,根据勾股定理求出P点坐标;在△DP1Q1 中,根据题意求出P点坐标;此题是综合题,难度较大,计算和解方程时需认真仔细.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【感受联系】在初二的数学学习中,我们感受过等腰三角形与直角三角形的密切联系.等腰三角形作底边上的高线可转化为直角三角形,直角三角形沿直角边翻折可得到等腰三角形等等.
(1)【探究发现】某同学运用这一联系,发现了“30°角所对的直角边等于斜边的一半”.并给出了如下的部分探究过程,请你补充完整证明过程
已知:如图,
在 △
△ 中,
中, 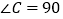 °,
°,  °.
°.
求证: .
.
(2)【灵活运用】该同学家有一张折叠方桌如图①所示,方桌的主视图如图②.经测得 ,
,  ,将桌子放平,两条桌腿叉开的角度
,将桌子放平,两条桌腿叉开的角度  .
.
求:桌面与地面的高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知在长方形ABCD中, AD=8, AB=4,将长方形ABCD沿着对角线BD折叠,使点C落在
 处,
处,  交AD于点E.
交AD于点E.
(1)求证:△BED是等腰三角形.
(2)求DE的长.
(3)如图2,若点P是BD上一动点,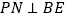 于点N,
于点N, 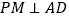 于点M,问: PN+PM的长是否为定值?如果是,请求出该值,如果不是,请说明理由.
于点M,问: PN+PM的长是否为定值?如果是,请求出该值,如果不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a3a2=a6
B.(a2b)3=a6b3
C.a8÷a2=a4
D.a+a=a2 -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式a2﹣ab2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列长度的三条线段能组成三角形的是( )
A. 5cm,6cm,11cmB. 1cm,3cm,5cmC. 2cm,3cm,6cmD. 3cm,4cm,5cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】据河南省发改委发布消息,2016年全省固定资产投资继续保持持续稳定增长,全年完成39753亿元,总量居全国第3位.将数据39753亿用科学记数法表示为( )
A.3.9753×109
B.0.39753×1010
C.39.753×1011
D.3.9753×1012
相关试题

