【题目】已知x轴上有点A(1,0),点B在y轴上,点C(m,0)为x轴上一动点且m<﹣1,连接AB,BC,tan∠ABO= ![]() ,以线段BC为直径作⊙M交直线AB于点D,过点B作直线l∥AC,过A,B,C三点的抛物线为y=ax2+bx+c,直线l与抛物线和⊙M的另一个交点分别是E,F.
,以线段BC为直径作⊙M交直线AB于点D,过点B作直线l∥AC,过A,B,C三点的抛物线为y=ax2+bx+c,直线l与抛物线和⊙M的另一个交点分别是E,F.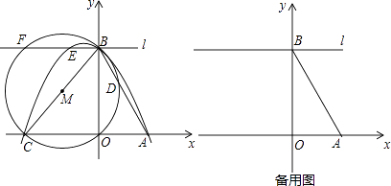
(1)求B点坐标;
(2)用含m的式子表示抛物线的对称轴;
(3)线段EF的长是否为定值?如果是,求出EF的长;如果不是,说明理由.
(4)是否存在点C(m,0),使得BD= ![]() AB?若存在,求出此时m的值;若不存在,说明理由.
AB?若存在,求出此时m的值;若不存在,说明理由.
参考答案:
【答案】
(1)
解:∵tan∠ABO= ![]() ,且A(1,0),
,且A(1,0),
∴OB=2,即:点B的坐标为(0,2)
(2)
解:点C(m,0),A(1,0),B(0,2)在抛物线y=ax2+bx+c上,
∴ 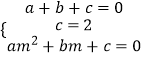
解之得:b=﹣ ![]() ,a=
,a= ![]() ,
,
∴x=﹣ ![]() =
= ![]() .
.
即:抛物线的对称轴为x= ![]()
(3)
解:∵点E在抛物线y=ax2+bx+c上,又在直线y=2上,
∴2=ax2+bx+2
∴x1=0,x2=﹣ ![]()
∴E(﹣ ![]() ,2),
,2),
又∵直线l∥x轴,BC是⊙M的直径,
∴BF∥OC,BF=OC,
∴F(m,2)
∴EF=﹣ ![]() ﹣m,
﹣m,
∵点C(m,0)为x轴上一动点且m<﹣1,
∴m的值是一个变量,
即:线段EF的长不是定值
(4)
解:如下图所示:连接CD
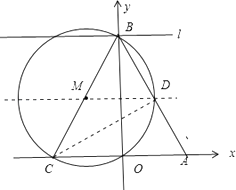
∵BCS是⊙M的直径,
∴∠CDB=90°,
∵若BD= ![]() AB,即BD=DA
AB,即BD=DA
则易证CB=CA
∴ ![]() =1﹣m
=1﹣m
解之得m=﹣ ![]() ,
,
即:存在一点C(﹣ ![]() ,0),使得BD=
,0),使得BD= ![]() AB
AB
【解析】(1)根据正切函数的定义及点A的坐标求解;(2)因为点C、A、B在抛物线上,故代入其坐标列方程组求解即可;(3)点E(x,y)既在抛物线y=ax2+bx+2上,又在直线y=2上,所以有2=ax2+bx+2,由此可知E(﹣ ![]() ,2),又因为直线l∥x轴,BC是⊙M的直径,由圆的对称性可知BF∥OC且BF=OC,所以F(m,2),由此可分析EF长;(4)连接CD,因为BC为圆的直径,所以∠BDC=90°,若BD=
,2),又因为直线l∥x轴,BC是⊙M的直径,由圆的对称性可知BF∥OC且BF=OC,所以F(m,2),由此可分析EF长;(4)连接CD,因为BC为圆的直径,所以∠BDC=90°,若BD= ![]() AB,可证明CA=CB,由此可求得符合题意的点C(﹣
AB,可证明CA=CB,由此可求得符合题意的点C(﹣ ![]() ,0).
,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】请根据图中提供的信息,回答下列问题

(1)一个暖瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的暖瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定: 这两种商品都打九折;乙商场规定:买一个暖瓶赠送一个水杯。若某单位想要买4个暖瓶和15个水杯,请问选择哪家商场购买更合算,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】周末,小明,小红等同学随父母一同去某景点旅游,在购买门票时,小明和小红有图1所示的对话,根据图2的门票票价和图1所示的对话内容完成下列问题.
(1)他们一共去了几个成人几个学生?
(2)请你帮他们算一算,用哪种方式买票更省钱,省多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】由若干边长为1的小正方形拼成一系列“L”形图案(如图1).

(1)当“L”形由7个正方形组成时,其周长为;
(2)如图2,过格点D作直线EF,分别交AB,AC于点E,F.
①试说明AEAF=AE+AF;
②若“L”形由n个正方形组成时,EF将“L”形分割开,直线上方的面积为整个“L”形面积的一半,试求n的取值范围以及此时线段EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点A的坐标为(-2,0),等边三角形AOC经过平移或轴对称或旋转对称都可以得到△OBD。
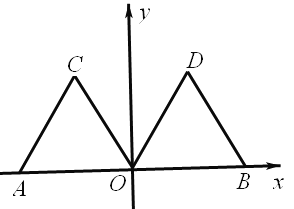
(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是 个单位长度;△AOC与△OBD关于直线对称,则对称轴是 ;△AOC绕原点O顺时针旋转得到△OBD,则旋转角可以是 度;
(2)连接AD,交OC于点E,求∠AEO的度数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴是初中数学的一个重要工具.利用数轴可以将数与形完美的结合.研究数轴我们发现了许多重要的规律:数轴上A点、B点表示的数为a、b,则A,B两点之间的距离AB=|a﹣b|,若a>b,则可简化为AB=a﹣b.
如图:
已知数轴上有A、B两点,分别表示的数为﹣10,8,点A以每秒3个单位的速度沿数轴向右匀速运动,点B以每秒2个单位向左匀速运动.设运动时间为t秒(t>0).
(综合运用).
(1)点A运动2秒后所在位置的点表示的数为 ;点B运动3秒后所在位置的点表示的数为 ;
(2)它们按上述方式运动,A、B两点经过多少秒会相遇,相遇点所表示的数是什么?
(3)它们按上述方式运动,A、B两点经过多少秒后相距2个单位长度?
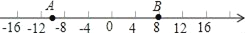
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种型号油电混合动力汽车,从A地到B地燃油行驶纯燃油费用76元,从A地到B地用电行驶纯电费用26元,已知每行驶1千米,纯燃油费用比纯用电费用多0.5元.
(1)求每行驶1千米纯用电的费用;
(2)若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元,则至少用电行驶多少千米?
相关试题

