【题目】数轴是初中数学的一个重要工具.利用数轴可以将数与形完美的结合.研究数轴我们发现了许多重要的规律:数轴上A点、B点表示的数为a、b,则A,B两点之间的距离AB=|a﹣b|,若a>b,则可简化为AB=a﹣b.
如图:
已知数轴上有A、B两点,分别表示的数为﹣10,8,点A以每秒3个单位的速度沿数轴向右匀速运动,点B以每秒2个单位向左匀速运动.设运动时间为t秒(t>0).
(综合运用).
(1)点A运动2秒后所在位置的点表示的数为 ;点B运动3秒后所在位置的点表示的数为 ;
(2)它们按上述方式运动,A、B两点经过多少秒会相遇,相遇点所表示的数是什么?
(3)它们按上述方式运动,A、B两点经过多少秒后相距2个单位长度?
![]()
参考答案:
【答案】(1) ﹣4;2.(2) A,B两点经过3.6秒后会相遇,相遇点所表示的数是0.8.(3) 经过3.2s或4s后A,B两点相距2个单位.
【解析】
(1)点A运动t秒后所在位置的点表示的数=运动开始前A点表示的数+点A运动的路程,点B运动t秒后所在位置的点表示的数=运动开始前B点表示的数-点B运动的路程;
(2)设它们按上述方式运动,A、B两点经过t秒会相遇,等量关系为:点A运动的路程+点B运动的路程=18,依此列出方程,解方程即可;
(3)分类讨论①若A点在左边,B点在右边,则8﹣2t﹣(﹣10+3t)=2,②若A点在右边,B点在左边,则﹣10﹣3t﹣(8﹣2t)=2,求解即可得出结论.
(1)﹣10+3×2=﹣4,8﹣2×3=2.
故答案为:﹣4;2.
(2)根据题意得:﹣10+3t=8﹣2t,
解得: t=3.6,
∴﹣10+3t=0.8.
答:A,B两点经过3.6秒后会相遇,相遇点所表示的数是0.8.
(3)分类讨论:
①若A点在左边,B点在右边,则8﹣2t﹣(﹣10+3t)=2,
解得:t=3.2;
②若A点在右边,B点在左边,则﹣10﹣3t﹣(8﹣2t)=2,
解得:t=4.
答:经过3.2s或4s后A,B两点相距2个单位.
-
科目: 来源: 题型:
查看答案和解析>>【题目】由若干边长为1的小正方形拼成一系列“L”形图案(如图1).

(1)当“L”形由7个正方形组成时,其周长为;
(2)如图2,过格点D作直线EF,分别交AB,AC于点E,F.
①试说明AEAF=AE+AF;
②若“L”形由n个正方形组成时,EF将“L”形分割开,直线上方的面积为整个“L”形面积的一半,试求n的取值范围以及此时线段EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知x轴上有点A(1,0),点B在y轴上,点C(m,0)为x轴上一动点且m<﹣1,连接AB,BC,tan∠ABO=
 ,以线段BC为直径作⊙M交直线AB于点D,过点B作直线l∥AC,过A,B,C三点的抛物线为y=ax2+bx+c,直线l与抛物线和⊙M的另一个交点分别是E,F.
,以线段BC为直径作⊙M交直线AB于点D,过点B作直线l∥AC,过A,B,C三点的抛物线为y=ax2+bx+c,直线l与抛物线和⊙M的另一个交点分别是E,F.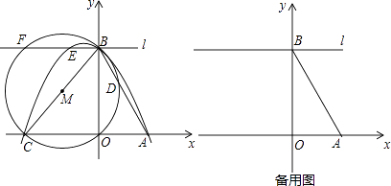
(1)求B点坐标;
(2)用含m的式子表示抛物线的对称轴;
(3)线段EF的长是否为定值?如果是,求出EF的长;如果不是,说明理由.
(4)是否存在点C(m,0),使得BD= AB?若存在,求出此时m的值;若不存在,说明理由.
AB?若存在,求出此时m的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点A的坐标为(-2,0),等边三角形AOC经过平移或轴对称或旋转对称都可以得到△OBD。
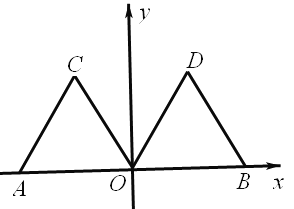
(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是 个单位长度;△AOC与△OBD关于直线对称,则对称轴是 ;△AOC绕原点O顺时针旋转得到△OBD,则旋转角可以是 度;
(2)连接AD,交OC于点E,求∠AEO的度数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种型号油电混合动力汽车,从A地到B地燃油行驶纯燃油费用76元,从A地到B地用电行驶纯电费用26元,已知每行驶1千米,纯燃油费用比纯用电费用多0.5元.
(1)求每行驶1千米纯用电的费用;
(2)若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元,则至少用电行驶多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分8分)如图,四边形ABCD中,
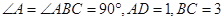 ,E是边CD的中点,连接BE并延长与AD的延长线相较于点F.
,E是边CD的中点,连接BE并延长与AD的延长线相较于点F.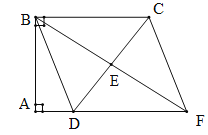
(1)求证:四边形BDFC是平行四边形;
(2)若△BCD是等腰三角形,求四边形BDFC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,菱形ABCD的顶点A的坐标为(2,0),点B的坐标为(0,1),点C在第一象限,对角线BD与x轴平行.直线y=x+4与x轴、y轴分别交于点E,F.将菱形ABCD沿x轴向左平移k个单位,当点C落在△EOF的内部时(不包括三角形的边),k的值可能是( )

A.2 B.3 C.4 D.5
相关试题

