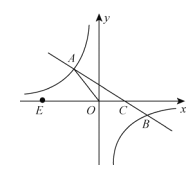
【题目】如图,在平面直角坐标系xoy中,一次函数y=kx+b(k≠0)的图象与反比例函数![]() (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n)。线段OA=5,E为x轴上一点,且
(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n)。线段OA=5,E为x轴上一点,且![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)求△AOC的面积;
(3)直接写出一次函数值大于反比例函数自变量x的取值范围。
参考答案:
【答案】(1) y=![]() ; y=
; y=![]() ;(2)6;(3) x<-3或0<x<6
;(2)6;(3) x<-3或0<x<6
【解析】试题分析:(1)过点A作AH⊥x轴于H点,由sin∠AOE=![]() ,OA=5,根据正弦的定义可求出AH,再根据勾股定理得到HO,即得到A点坐标(-3,4),把A(-3,4)代入y=
,OA=5,根据正弦的定义可求出AH,再根据勾股定理得到HO,即得到A点坐标(-3,4),把A(-3,4)代入y=![]() ,确定反比例函数的解析式;将B(6,n)代入,确定点B点坐标,然后把A点和B点坐标代入y=kx+b(k≠0),求出k和B即可;
,确定反比例函数的解析式;将B(6,n)代入,确定点B点坐标,然后把A点和B点坐标代入y=kx+b(k≠0),求出k和B即可;
(2)先令y=0,求出C点坐标,得到OC的长,然后根据三角形的面积公式计算△AOC的面积即可;
(3)观察图象可得当x<-3或0<x<6时,反比例函数图象都在一次函数图象的下方,即一次函数值大于反比例函数值.
试题解析:(1)过A作AH⊥x轴交x轴于H,
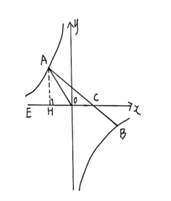
∵sin∠ACE=![]() =
=![]() ,OA=5,
,OA=5,
∴AH=4,∴OH=![]() =3,
=3,
∴A(-3,4),
将A(-3,4)代入y=![]() ,得m=-12,∴反比例函数的解析式为y=-
,得m=-12,∴反比例函数的解析式为y=-![]() ,
,
将B(6,n)代入y=-![]() ,得n=-2,
,得n=-2,
∴B(6,-2),
将A(-3,4)和B(6,-2)分别代入y=kx+b(k≠0),得![]() ,解得
,解得 ,
,
∴直线解析式:y=![]() ;
;
(2)在直线y=![]() 中,令y=0,则有
中,令y=0,则有![]() =0,解得x=3,
=0,解得x=3,
∴C(3,0),即OC=3,
∴![]() ;
;
(3)观察图象可得:当x<-3或0<x<6时,一次函数值大于反比例函数值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形的两边长为
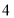 和
和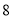 ,则它腰上的高长度为______.
,则它腰上的高长度为______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
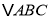 中,已知
中,已知 于点
于点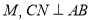 于点
于点 ,
, 为
为 边的中点,连接
边的中点,连接 ,则下列结论:①
,则下列结论:① ;②
;② ;③
;③ 为等边三角形;④当
为等边三角形;④当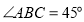 时,
时,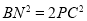 .其中正确的是____________(填写序号).
.其中正确的是____________(填写序号).
-
科目: 来源: 题型:
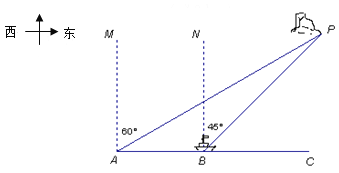
查看答案和解析>>【题目】海中有一个小岛P,它的周围18海里内有暗礁,渔船跟踪鱼群由西向东航行,在点A测得小岛P在北偏东60°方向上,航行12海里到达B点,这时测得小岛P在北偏东45°方向上.如果渔船不改变航线继续向东航行,有没有触礁危险?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知:如图①,直线MN⊥直线PQ,垂足为O,点A在射线OP上,点B在射线OQ上(A、B不与O点重合),点C在射线ON上,过点C作直线
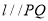 ,点D在点C的左边。
,点D在点C的左边。(1)若BD平分∠ABC,
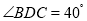 ,则
,则 _____°;
_____°;(2)如图②,若
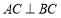 ,作∠CBA的平分线交OC于E,交AC于F,试说明
,作∠CBA的平分线交OC于E,交AC于F,试说明 ;
;(3)如图③,若∠ADC=∠DAC,点B在射线OQ上运动,∠ACB的平分线交DA的延长线于点H.在点B运动过程中
 的值是否变化?若不变,求出其值;若变化,求出变化范围.
的值是否变化?若不变,求出其值;若变化,求出变化范围.
-
科目: 来源: 题型:
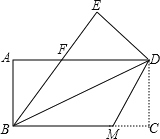
查看答案和解析>>【题目】如图,把一张矩形的纸ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F.
⑴求证:ΔABF≌ΔEDF;
⑵若将折叠的图形恢复原状,点F与BC边上的点M正好重合,连接DM,试判断四边形BMDF的形状,并说明理由.
-
科目: 来源: 题型:
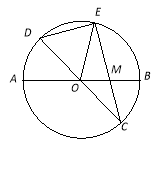
查看答案和解析>>【题目】已知:如图,在半径为4的⊙O中,AB、CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连结DE,DE=
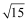 .
.(1)求证:
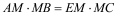 ;
;(2)求EM的长;
(3)求sin∠EOB的值.
相关试题

