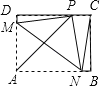
【题目】如图,在长方形纸片ABCD中,AB=12厘米,折叠纸片,使得点A落在CD边上的点P处,折痕为MN,点M、N分别在边AD、AB上,当点P恰好是CD边的中点时,点N与点B重合,若在折叠过程中NP=NC,则PD=_____.
参考答案:
【答案】9cm
【解析】
利用点P是CD的中点及勾股定理求出BC的长,由NP=NC,过点N作HN⊥CD,利用勾股定理求出NB,再根据等腰三角形的性质得到PC即可求得PD.
如图1,当点P恰好是CD边的中点时,点N与点B重合,
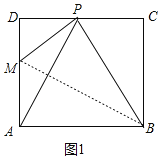
∵点P是CD的中点,
∴CP=![]() CD=6cm,
CD=6cm,
由折叠的性质可得:AB=PB=12cm,
∴BC=![]() ,
,
如图2,折叠过程中NP=NC,过点N作HN⊥CD,
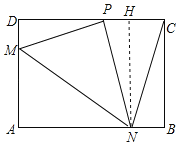
由折叠的性质可得:AN=PN=NC,
∵NB2+BC2=NC2,
∴NB2+108=(12﹣NB)2,
∴NB=![]() cm,
cm,
∵NH⊥CD,∠ABC=∠BCD=90°,
∴四边形BCHN是矩形,
∴HC=BN=![]() cm,
cm,
∵NC=NP,NH⊥CD,
∴PC=2HC=3cm,
∴DP=CD﹣PC=9cm,
故答案为:9cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1:y=kx+b与x轴、y轴分别交于A,B两点,其中点B的坐标为(0,6),∠BAO=30°将直线l1沿着y轴正方向平移一段距离得到直线l2交y轴于点M,且l1与l2之间的距离为3,点C(x,y)是直线11上的一个动点,过点C作AB的垂线CD交y轴于点D.
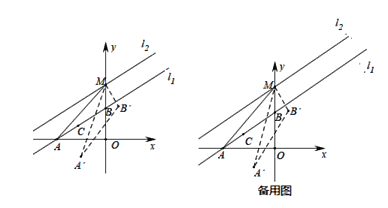
(1)求点M的坐标和直线l1的解析式;
(2)当C运动到什么位置时,△AOD的面积为21
 ,求出此时点C的坐标;
,求出此时点C的坐标;(3)连接AM,将△ABM绕着点M旋转得到△A'B'M,在平面内是否存在一点N.使四边形AMA'N为矩形?若存在,求出点N的坐标:若不存在,请说明理由.
-
科目: 来源: 题型:
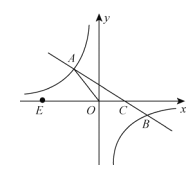
查看答案和解析>>【题目】如图,在平面直角坐标系xoy中,一次函数y=kx+b(k≠0)的图象与反比例函数
 (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n)。线段OA=5,E为x轴上一点,且
(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n)。线段OA=5,E为x轴上一点,且 .
.(1)求该反比例函数和一次函数的解析式;
(2)求△AOC的面积;
(3)直接写出一次函数值大于反比例函数自变量x的取值范围。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题:①所有锐角三角函数值都为正数;②解直角三角形时只需已知除直角外的两个元素;③Rt△ABC中,∠B=90°,则sin2A+cos2A=1;④Rt△ABC中,∠A=90°,则tanCsinC=cosC.其中正确的命题有( )
A. 0个 B. 1个 C. 2个 D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘海轮位于灯塔P的北偏东方向55°,距离灯塔为2海里的点A处.如果海轮沿正南方向航行到灯塔的正东位置,海轮航行的距离AB长是( )

A. 2海里 B. 2sin 55°海里
C. 2cos 55°海里 D. 2tan 55°海里
-
科目: 来源: 题型:
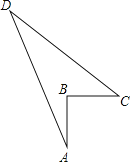
查看答案和解析>>【题目】如图,一块形如四边形ABCD的草地中,AB=3m,BC=4m,CD=12m,DA=13m,且∠ABC=90°,要以AC、CD、DA为边制作围栏,问围栏长多少米,草地面积多大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程组解应用题:用3辆
 型车和2辆
型车和2辆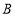 型车载满货物一次可运货17吨;用2辆
型车载满货物一次可运货17吨;用2辆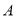 型车和3辆
型车和3辆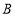 型车载满货物一次可运货18吨,某物流公司现有35吨货物,计划同时租用
型车载满货物一次可运货18吨,某物流公司现有35吨货物,计划同时租用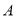 型车
型车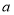 辆,
辆,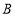 型车
型车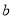 辆,一次运完,且恰好每辆车都载满货物.
辆,一次运完,且恰好每辆车都载满货物.(1)1辆
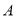 型车和1辆
型车和1辆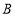 型车都载满货物一次可分别运货多少吨?
型车都载满货物一次可分别运货多少吨?(2)若
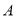 型车每辆需租金200元/次,
型车每辆需租金200元/次,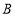 型车每辆需租金240元/次,请你帮该物流设计最省钱的租车方案,并求出最少租车费.
型车每辆需租金240元/次,请你帮该物流设计最省钱的租车方案,并求出最少租车费.
相关试题

