搜索
【题目】在抗击“新冠肺炎”时期，开展停课不停学活动，戴老师从3月1号到7号在网上答题个数记录如下
日期 | 1号 | 2号 | 3号 | 4号 | 5号 | 6号 | 7号 |
答题个数 | 68 | 55 | 50 | 56 | 54 | 48 | 68 |
在戴老师每天的答题个数所组成的这组数据中，众数和中位数依次是（）
A.68，55B.55，68C.68，57D.55，57
参考答案：
【答案】A
【解析】
根据众数和中位数的求解方法进行计算后，再进行判定即可．
这组数据：68，55，50，56，54，48，68中出现次数最多的为68，故众数是68；
把这组数据从小到大排列为：48，50，54，55，56，68，68中间的数据为55，故中位数是55．
故选：A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商店需要购进甲、乙两种商品共180件，其进价和售价如表：（注：获利=售价﹣进价）
甲
乙
进价（元/件）
14
35
售价（元/件）
20
43
（1）若商店计划销售完这批商品后能获利1240元，问甲、乙两种商品应分别购进多少件？
（2）若商店计划投入资金少于5040元，且销售完这批商品后获利多于1312元，请问有哪几种购货方案？并直接写出其中获利最大的购货方案． -
科目： 来源： 题型：
查看答案和解析>>【题目】一次函数y＝kx﹣3k+1的图象必经过一个定点，该定点的坐标是_____
-
科目： 来源： 题型：
查看答案和解析>>【题目】某地区在一次九年级数学做了检测中，有一道满分8分的解答题，按评分标准，所有考生的得分只有四种：0分，3分，5分，8分．老师为了了解学生的得分情况与题目的难易情况，从全区4500名考生的试卷中随机抽取一部分，通过分析与整理，绘制了如下两幅图不完整的统计图．
请根据以上信息解答下列问题：
（1）填空：a= ，b= ，并把条形统计图补全；
（2）请估计该地区此题得满分（即8分）的学生人数；
（3）已知难度系数的计算公式为L=
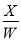，其中L为难度系数，X为样本平均得分，W为试题满分值．一般来说，根据试题的难度系数可将试题分为以下三类：当0＜L≤0.4时，此题为难题；当0.4＜L≤0.7时，此题为中等难度试题；当0.7＜L＜1时，此题为容易题．试问此题对于该地区的九年级学生来说属于哪一类？
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校食堂的中餐与晚餐的资费标准如下：
种类
单价
米饭
0.5元/份
A类套餐菜
3.5元/份
B类套餐菜
2.5元/份
小杰同学某星期从周一到周五每天的中餐与晚餐均在学校选用A类或B类中的一份套餐菜与一份米饭用餐，这五天共消费36元．请问小杰在这五天内，A，B类套餐菜各选用了多少次？
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列计算结果正确的是（ ）
A.﹣2x2y3x3y3＝﹣2x6y9B.12x6y4÷2x3y3＝6x3y
C.3x3y2﹣x2y3＝xyD.（﹣2a﹣3）（2a﹣3）＝4a2﹣9
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，抛物线C：y=x2经过变化可得到抛物线C1：y1=a1x（x﹣b1），C1与x轴的正半轴交与点A1，且其对称轴分别交抛物线C，C1于点B1，D1，此时四边形OB1A1D1恰为正方形；按上述类似方法，如图2，抛物线C1：y1=a1x（x﹣b1）经过变换可得到抛物线C2：y2=a2x（x﹣b2），C2与x轴的正半轴交与点A2，且其对称轴分别交抛物线C1，C2于点B2，D2，此时四边形OB2A2D2也恰为正方形；按上述类似方法，如图3，可得到抛物线C3：y3=a3x（x﹣b3）与正方形OB3A3D3．请探究以下问题：
（1）填空：a1= ，b1= ；
（2）求出C2与C3的解析式；
（3）按上述类似方法，可得到抛物线Cn：yn=anx（x﹣bn）与正方形OBnAnDn（n≥1）．
①请用含n的代数式直接表示出Cn的解析式；
②当x取任意不为0的实数时，试比较y2015与y2016的函数值的大小并说明理由．
相关试题
