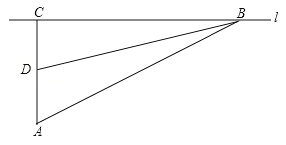
【题目】校车安全是近几年社会关注的热点问题,安全隐患主要是超速和超载.某中学九年级数学活动小组进行了测试汽车速度的实验,如图,先在笔直的公路l旁选取一点A,在公路l上确定点B、C,使得AC⊥l,∠BAC=60°,再在AC上确定点D,使得∠BDC=75°,测得AD=40米,已知本路段对校车限速是50千米/时,若测得某校车从B到C匀速行驶用时10秒,问这辆车在本路段是否超速?请说明理由(参考数据:![]() =1.41,
=1.41,![]() =1.73)
=1.73)
参考答案:
【答案】解:过点D作DE⊥AB于点E,
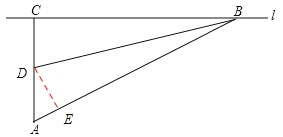
∵∠CDB=75°,∠BAC=60°,∴∠CBD=15°,∠EBD=15°。
在Rt△CBD和Rt△EBD中,
∵∠CBD=∠EBD,∠DCB =∠DEB,BD=BD,
∴△CBD≌△EBD(AAS)。
∴CD=DE。
在Rt△ADE中,∠A=60°,AD=40米,
∴DE=ADsin60°=20![]() 米,
米,
∴AC=AD+CD=AD+DE=(40+20![]() )米,
)米,
在Rt△ABC中,BC=ACtan∠A=(40![]() +60)米,
+60)米,
∴速度=![]() (米/秒)。
(米/秒)。
∵12.92米/秒=46.512千米/小时<50千米/时,∴该车没有超速。
【解析】
试题过点D作DE⊥AB于点E,证明△BCD≌△BED,在Rt△ADE中求出DE,继而得出CD,计算出AC的长度后,在Rt△ABC中求出BC,继而可判断是否超速。
-
科目: 来源: 题型:
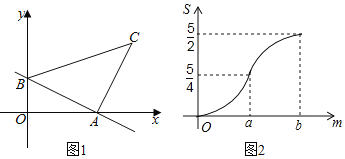
查看答案和解析>>【题目】如图1,直线AB与x轴、y轴分别相交于点A、B,将线段AB绕点A顺时针旋转90°,得到AC,连接BC,将△ABC沿射线BA平移,当点C到达x轴时运动停止.设平移距离为m,平移后的图形在x轴下方部分的面积为S,S关于m的函数图象如图2所示(其中0<m≤a,a<m≤b时,函数的解析式不同).
(1)填空:△ABC的面积为 ;
(2)求直线AB的解析式;
(3)求S关于m的解析式,并写出m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小明遇到这样一个问题:
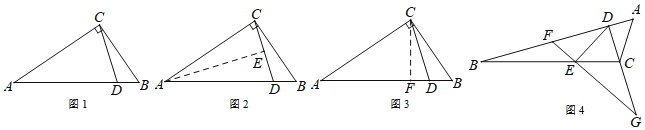
如图1,△ABC中,∠ACB=90°,点D在AB上,且∠BAC=2∠DCB,求证:AC=AD.
小明发现,除了直接用角度计算的方法外,还可以用下面两种方法:
方法1:如图2,作AE平分∠CAB,与CD相交于点E.
方法2:如图3,作∠DCF=∠DCB,与AB相交于点F.
(1)根据阅读材料,任选一种方法,证明AC=AD.
用学过的知识或参考小明的方法,解决下面的问题:
(2)如图4,△ABC中,点D在AB上,点E在BC上,且∠BDE=2∠ABC,点F在BD上,且∠AFE=∠BAC,延长DC、FE,相交于点G,且∠DGF=∠BDE.
①在图中找出与∠DEF相等的角,并加以证明;
②若AB=kDF,猜想线段DE与DB的数量关系,并证明你的猜想.
-
科目: 来源: 题型:
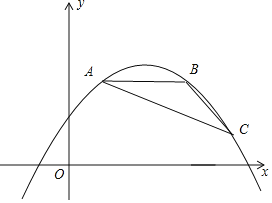
查看答案和解析>>【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣
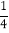 <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,梯形
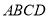 中,上底
中,上底 下底
下底 高
高 梯形的面积
梯形的面积 动点
动点 从点
从点 出发,沿
出发,沿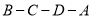 方向,以每秒
方向,以每秒 个单位长度的速度匀速运动.
个单位长度的速度匀速运动.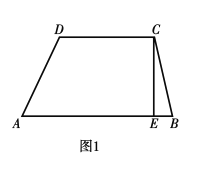
 请根据
请根据 与
与 的关系式,完成下列问题:
的关系式,完成下列问题:




···





···
 补充表格中的数据;
补充表格中的数据;  当
当 时,表示的图形是_ .
时,表示的图形是_ . 梯形的面积
梯形的面积 与
与 的关系如图2所示,则点
的关系如图2所示,则点 表示的实际意义是_ ;
表示的实际意义是_ ;
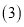 若点
若点 运动的时间为
运动的时间为 的面积为
的面积为 与
与 的关系如图3所示.求
的关系如图3所示.求 的长和
的长和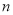 的值.
的值.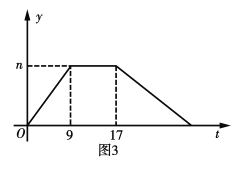
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等边三角形
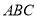 中
中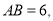 点
点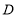 是
是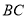 边上的一点,点
边上的一点,点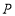 是
是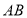 边上的一点,连接
边上的一点,连接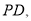 以
以 为边作等边三角形
为边作等边三角形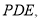 连接
连接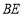 .
.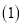 如图1,当点
如图1,当点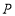 与点
与点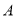 重合时,
重合时,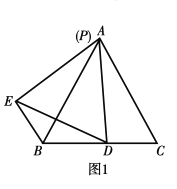
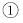 找出图中的一对全等三角形,并证明;
找出图中的一对全等三角形,并证明;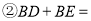 ;
; 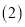 如图2,若
如图2,若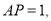 请计算
请计算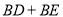 的值.
的值.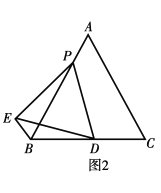
-
科目: 来源: 题型:
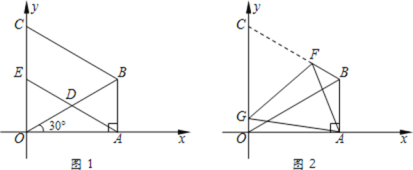
查看答案和解析>>【题目】如图1,在△ABO中,∠OAB=90°,∠AOB=30°,OB=8.以OB为一边,在△OAB外作等边三角形OBC,D是OB的中点,连接AD并延长交OC于E.
(1)求点B的坐标;
(2)求证:四边形ABCE是平行四边形;
(3)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.
相关试题

