【题目】已知∠AOB=120°,∠COD=60°,OE平分∠BOC
(1)如图①.当∠COD在∠AOB的内部时
①若∠AOC=39°40′,求∠DOE的度数;
②若∠AOC=α,求∠DOE的度数(用含α的代数式表示),
(2)如图②,当∠COD在∠AOB的外部时,
①请直接写出∠AOC与∠DOE的度数之间的关系;
②在∠AOC内部有一条射线OF,满足∠AOC+2∠BOE=4∠AOF,写出∠AOF与∠DOE的度数之间的关系.

参考答案:
【答案】(1)①19°50′;②∠DOE=![]() ;(2)①∠AOC=2∠DOE;②∠DOE=∠AOF+30°.
;(2)①∠AOC=2∠DOE;②∠DOE=∠AOF+30°.
【解析】
(1)①②根据角平分线的定义和角的和差即可得到结论;
②根据角平分线的定义和角的和差即可得到结论;
(2)①根据已知条件得到∠AOC=120°+∠BOC,∠DOE=60°+∠COE,根据角平分线的定义得到∠COE=![]() ∠BOC,等量代换即可得到结论;
∠BOC,等量代换即可得到结论;
②如图,由①知,∠AOC=2∠DOE,根据∠AOC+2∠BOE=4∠AOF,化简即可得到结论.
(1)①∵∠AOB=120°,∠COD=60°,∠AOC=39°40′,
∴∠BOC=∠AOB﹣∠AOC=120°﹣39°40′=80°20′,
∵OE平分∠BOC,
∴∠COE=![]() ∠BOC=40°10′,
∠BOC=40°10′,
∴∠DOE=∠COD﹣∠COE=19°50′;
②∵∠AOB=120°,∠COD=60°,∠AOC=α,
∴∠BOC=∠AOB﹣∠AOC=120°﹣α,
∵OE平分∠BOC,
∴∠COE=![]() ∠BOC=60°﹣
∠BOC=60°﹣![]() α,
α,
∴∠DOE=![]() ;
;
(2)①∵∠AOC=120°+∠BOC,∠DOE=60°+∠COE,
∵OE平分∠BOC,
∴∠COE=![]() BOC,
BOC,
∴∠AOC=2∠DOE;
②如图,
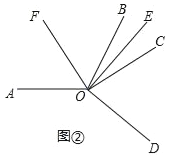
由①知,∠AOC=2∠DOE,
∵∠AOC+2∠BOE=4∠AOF,
∴∠AOC+∠BOC=∠AOC+∠AOC﹣120°=2∠AOC﹣120°=4∠DOE﹣120°=4∠AOF,
∴∠DOE=∠AOF+30°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1+∠2=180°,∠B=∠D.说明AB∥CD的理由.
补全下面的说理过程,并在括号内填上适当的理由
解:∵∠1+∠2=180°(已知)
∠2=∠AHB( )
∴ (等量代换)
∴DE∥BF( )
∴∠D=∠ ( )
∵∠ =∠B(等量代换)
∴AB∥CD( )
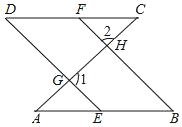
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O为原点,已知数轴上点A和点B所表示的数分别为﹣10和6,动点P从点A出发,以每秒6个单位长度的速度沿数轴正方向匀速运动,同时动点Q从点B出发,以每秒3个单位的速度沿数轴负方向匀速运动,设运动时间为t(t>0)秒
(1)当t=2时,求AP的中点C所对应的数;
(2)当PQ=OA时,求点Q所对应的数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店第一次用600元购进2B铅笔若干支,第二次又用600元购进该款铅笔,但这次每支的进价是第一次进价的
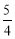 倍,购进数量比第一次少了30支.
倍,购进数量比第一次少了30支.(1)求第一次每支铅笔的进价是多少元?
(2)若要求这两次购进的铅笔按同一价格全部销售完毕后获利不低于420元,问每支售价至少是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AC,AE=AF,BE与CF交于点D,则对于下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分线上.其中正确的是( )
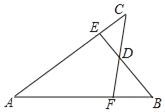
A. ① B. ② C. ①和② D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:AD平分∠CAE,AD∥BC.
(1)求证:△ABC是等腰三角形.
(2)当∠CAE等于多少度时△ABC是等边三角形?证明你的结论.
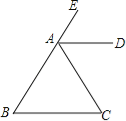
-
科目: 来源: 题型:
查看答案和解析>>【题目】规定:logab(a>0,a≠1,b>0)表示a,b之间的一种运算.
现有如下的运算法则:lognan=n.logNM=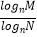 (a>0,a≠1,N>0,N≠1,M>0).
(a>0,a≠1,N>0,N≠1,M>0).
例如:log223=3,log25=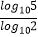 ,则log1001000=
,则log1001000=
相关试题

