【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E,H分别在AB,AC上,已知BC=40cm,AD=30cm.
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长与面积.

参考答案:
【答案】(1)详见解析;(2)正方形EFGH的边长为![]() cm,面积为
cm,面积为![]() cm2.
cm2.
【解析】试题分析:(1)由正方形可得EH∥BC,所以可以得到对应的两组角相等,即可证明相似;(2)设正方形边长为x,再由△AEH∽△ABC得到对应边成比例,列出关于x的方程,解出x即可.
试题解析:
(1)证明:∵四边形EFGH是正方形,∴EH∥BC,∴∠AEH=∠B,∠AHE=∠C,∴△AEH∽△ABC;
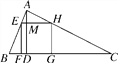
(2)解:∵∠EFD=∠FEM=∠FDM=90°,∴四边形EFDM是矩形,∴EF=DM.设正方形EFGH的边长为xcm,∵△AEH∽△ABC,∴ ![]() ,∴
,∴![]() ,解得x=
,解得x=![]() .
.
∴正方形EFGH的边长为![]() cm,面积为
cm,面积为![]() cm2.
cm2.
点睛:两个三角形的相似比等于对应的高之比,角平分线之比,中线之比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面上点P到圆周上的点的最长距离为8,最短距离为4,则此圆的半径为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简﹣2+3的结果是( )
A.﹣1
B.1
C.﹣5
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,∠ABC=90°,AB=3,BC=4,点Q是线段AC上的一个动点,过点Q作AC的垂线交线段AB(如图①)或线段AB的延长线(如图②)于点P.
(1)当点P在线段AB上时,求证:△AQP∽△ABC;
(2)当△PQB为等腰三角形时,求AP的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,则B,C两点的坐标分别是( )

A. (
 ,3),(-
,3),(- ,4) B. (
,4) B. (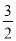 ,3),(-
,3),(- ,4)
,4)C. (
 ,
,  ),(-
),(- ,4) D. (
,4) D. ( ,
,  ),(-
),(- ,4)
,4) -
科目: 来源: 题型:
查看答案和解析>>【题目】点 P(﹣4,﹣3)所在的象限是( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C为直角,CD⊥AB于点D,BC=3,AB=5,写出其中的一对相似三角形是 和 ,它们的相似比为 .

相关试题

