【题目】如图,平面直角坐标系中,四边形OABC是长方形,O为原点,点A在x轴上,点C在y轴上且A(10,0),C(0,6),点D在AB边上,将△CBD沿CD翻折,点B恰好落在OA边上的点E处.
(1)求点E、点D的坐标;
(2)求折痕CD所在直线的函数表达式;
(3)请你延长直线CD交x轴于点F,点P是坐标轴上一点请直接写出使S△CEP=![]() S△COF的点P的坐标.
S△COF的点P的坐标.

参考答案:
【答案】⑴E(8,0)、D(10,![]() );⑵CD所在直线的解析式为:y=-
);⑵CD所在直线的解析式为:y=-![]() x+6;⑶点P的坐标为(2,0)或(14,0)或(0,
x+6;⑶点P的坐标为(2,0)或(14,0)或(0,![]() )或(0,
)或(0,![]() ).
).
【解析】
(1)由折叠的性质,可得CE=CB=10,在在直角△COE中,由勾股定理求得OE的长,确定E的坐标,设DA=x,则DE=6-x,AE=10-OE=2,运用勾股定理即可确定D的纵坐标,横坐标与点A 相同;
(2)C(0,6),D(10,![]() ),利用待定系数法求CD所在直线的解析式;
),利用待定系数法求CD所在直线的解析式;
(3)由(2)得到CD的解析式,令y=0,解得x=18,即F的坐标为(18,0),则△COF的面积为![]() OC×OF;当P在x轴上,设P的坐标为(a,0),则三角形CEP的高为OC,底为8-a,那么面积为
OC×OF;当P在x轴上,设P的坐标为(a,0),则三角形CEP的高为OC,底为8-a,那么面积为![]() OC×(8-a);当P在y轴上,设P的坐标为(0,b),则三角形CEP的高为OE,底为6-b,那么面积为
OC×(8-a);当P在y轴上,设P的坐标为(0,b),则三角形CEP的高为OE,底为6-b,那么面积为![]() OE×(6-b);分别结合三角形COF的面积求解即可.
OE×(6-b);分别结合三角形COF的面积求解即可.
解:⑴由折叠的性质,可得CE=CB=10,∠CED=90°
又∵OC=6
∴OE=![]()
∴EA=10-8=2
设DA=x,则DE=6-x,
在Rt△EDA中,由勾股定理得:
![]() 解得x=
解得x=![]()
∴E(8,0)、D(10,![]() );
);
⑵由题意得:C(0,6),D(10,![]() )
)
设CD所在的函数解析式为y=kx+b
则有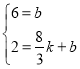 解得
解得![]()
CD所在直线的解析式为:y=-![]() x+6;
x+6;
⑶如图:

由(2)得CD的解析式y=-![]() x+6;令y=0,解得x=18,即F的坐标为(18,0)
x+6;令y=0,解得x=18,即F的坐标为(18,0)
∴OF=18
∴△COF的面积为![]() OC×OF=
OC×OF=![]() ×6×18=54
×6×18=54
∴S△CEP=![]() S△COF=18
S△COF=18
①当P在x轴上,设P的坐标为(a,0),则三角形CEP的高为OC,底为|8-a |,那么面积为![]() OC×(8-a)=18,即
OC×(8-a)=18,即![]() ×6×|8-a |=18,解得a=2或a=14,
×6×|8-a |=18,解得a=2或a=14,
∴P的坐标为(2,0)或(14,0)
②设P的坐标为(0,b),则三角形CEP的高为OE,底为6-b,
△CEP面积为![]() OE×|6-b|=18;
OE×|6-b|=18;
即![]() ×8×|6-b|=18;
×8×|6-b|=18;
解得b=![]() 或b=
或b=![]()
点P的坐标为(0,![]() )或(0,
)或(0,![]() ).
).
综上,P的坐标为(2,0)或(14,0)或(0,![]() )或(0,
)或(0,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】有A、B两个港口,水由A流向B,水流的速度是4千米/小时,甲、乙两船同时由A顺流驶向B,各自不停地在A、B之间往返航行,甲在静水中的速度是28千米/小时,乙在静水中的速度是20千米/小时.

设甲行驶的时间为t小时,甲船距B港口的距离为S1千米,乙船距B港口的距离为S2千米,如图为S1(千米)和t(小时)函数关系的部分图象.
(1)A、B两港口距离是_____千米.
(2)在图中画出乙船从出发到第一次返回A港口这段时间内,S2(千米)和t(小时)的函数关系的图象.
(3)求甲、乙两船第二次(不算开始时甲、乙在A处的那一次)相遇点M位于A、B港口的什么位置?
-
科目: 来源: 题型:
查看答案和解析>>【题目】乐乐根据学习函数的经验,对函数y=|x-1|的图象与性质进行了研究,下面是乐乐的研究过程,请补充完成:
(1)函数y=|x-1|的自变量x的取值范围是 .
(2)列表,找出y与x的几组对应值.
x
…
-1
0
1
2
3
…
y
…
b
1
0
1
2
…
(3)在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象.
(4)①函数的最小值为 ;
②写出一条该函数的其它性质: .

-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副直角三角板如图摆放,等腰直角三角板ABC的斜边BC与含30°角的直角三角板DBE的直角边BD长度相同,且斜边BC与BE在同一直线上,AC与BD交于点O,连接CD.
求证:△CDO是等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,G是边长为4的正方形ABCD的边BC上的一点,矩形DEFG的边EF过A,GD=5.
(1)指出图中所有的相似三角形;
(2)求FG的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,弦CD平分∠ACB,点E为弧AD上一点,连接CE、DE,CD与AB交于点N.
(1)如图1,求证:∠AND=∠CED;
(2)如图2,AB为⊙O直径,连接BE、BD,BE与CD交于点F,若2∠BDC=90°﹣∠DBE,求证:CD=CE;
(3)如图3,在(2)的条件下,连接OF,若BE=BD+4,BC=
 ,求线段OF的长.
,求线段OF的长.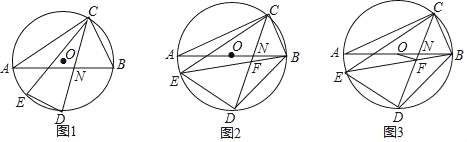
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D,E是等边三角形ABC的边BC,AC上的点,且CD=AE,AD交BE于点P,BQ⊥AD于点Q,已知PE=2,PQ=6,则AD等于( )

A.10B.12C.14D.16
相关试题

