Question

【题目】乐乐根据学习函数的经验，对函数y=|x-1|的图象与性质进行了研究，下面是乐乐的研究过程，请补充完成:

(1)函数y=|x-1|的自变量x的取值范围是 .

(2)列表，找出y与x的几组对应值.

x	…	-1	0	1	2	3	…
y	…	b	1	0	1	2	…

(3)在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点，并画出该函数的图象.

(4)①函数的最小值为 ；

②写出一条该函数的其它性质: .

Answer 1

【答案】（1）任何实数；（2）2；（3）见解析；（4）函数的最小值是0．

【解析】

（1）根据函数解析式得出即可；

（2）把x=-1代入，即可求出答案；

（3）画出图象即可；

（4）根据图象得出正确信息即可（答案不唯一）

解：⑴自变量x为任何实数，故答案为：任何实数；

⑵当x=-1时，b=|-1-1|=2，故答案为：2；

⑶如图.

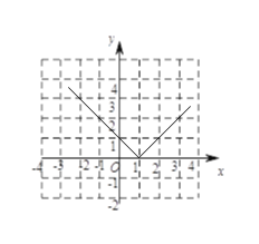
⑷函数的最小值是0，故答案为：函数的最小值是0．