搜索
【题目】如图，G是边长为4的正方形ABCD的边BC上的一点，矩形DEFG的边EF过A，GD=5．
（1）指出图中所有的相似三角形；
（2）求FG的长．
参考答案：
【答案】（1）△AFH，△DCG，△DEA，△GBH均是相似三角形；（2）FG=
．
【解析】
（1）根据都是直角，其余两个角加起来为90°，根据对顶角、余角等关系，可以看出△AFH，△DCG，△DEA，△GBH均是相似三角形．
（2）根据
，可以求出FG，由ED=FG，只要求出
＝
即可，因为△DEA∽△DCG，可以求出．
解:（1）△AFH，△DCG，△DEA，△GBH均是相似三角形；
（2）由∠E=∠C=90°，∠EDA与∠CDG均
为∠ADG的余角，得△DEA∽△DCG
∴＝，ED=FG，
∴，
由已知GD=5，AD=CD=4，
∴
，即FG=．
-
科目： 来源： 题型：
查看答案和解析>>【题目】乐乐根据学习函数的经验，对函数y=|x-1|的图象与性质进行了研究，下面是乐乐的研究过程，请补充完成:
(1)函数y=|x-1|的自变量x的取值范围是 .
(2)列表，找出y与x的几组对应值.
x
…
-1
0
1
2
3
…
y
…
b
1
0
1
2
…
(3)在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点，并画出该函数的图象.
(4)①函数的最小值为 ；
②写出一条该函数的其它性质: .
-
科目： 来源： 题型：
查看答案和解析>>【题目】将一副直角三角板如图摆放，等腰直角三角板ABC的斜边BC与含30°角的直角三角板DBE的直角边BD长度相同，且斜边BC与BE在同一直线上，AC与BD交于点O，连接CD．
求证：△CDO是等腰三角形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，平面直角坐标系中，四边形OABC是长方形，O为原点，点A在x轴上，点C在y轴上且A(10，0)，C(0，6)，点D在AB边上，将△CBD沿CD翻折，点B恰好落在OA边上的点E处.
(1)求点E、点D的坐标；
(2)求折痕CD所在直线的函数表达式；
(3)请你延长直线CD交x轴于点F，点P是坐标轴上一点请直接写出使S△CEP=
S△COF的点P的坐标.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC内接于⊙O，弦CD平分∠ACB，点E为弧AD上一点，连接CE、DE，CD与AB交于点N．
（1）如图1，求证：∠AND=∠CED；
（2）如图2，AB为⊙O直径，连接BE、BD，BE与CD交于点F，若2∠BDC=90°﹣∠DBE，求证：CD=CE；
（3）如图3，在（2）的条件下，连接OF，若BE=BD+4，BC=
，求线段OF的长．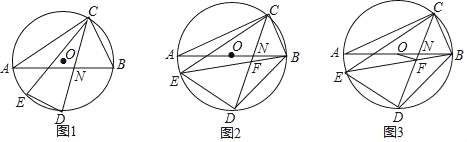
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点D，E是等边三角形ABC的边BC，AC上的点，且CD=AE，AD交BE于点P，BQ⊥AD于点Q，已知PE=2，PQ=6，则AD等于( )
A.10B.12C.14D.16
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC和△CDE都是等边三角形，B，C，D三点在一条直线上，AD与BE交于点P，AC，BE交于点M，AD，CE交于点N，连接MN，则下列五个结论：①AD=BE；②∠BMC=∠ANE；③∠APM=60°；④AN=BM；⑤△CMN是等边三角形．其中一定正确的是__________．（填出所有正确结论的序号）
相关试题
