搜索
【题目】在下面的图形中，对称轴条数最少的图形是（ ）
A.圆B.长方形C.正三角形D.正六边形
参考答案：
【答案】B
【解析】
根据轴对称图形的定义，分别找出题干中的图形的所有对称轴条数，即可进行判断．
A、圆有无数条对称轴，
B、长方形有2条对称轴，
C、正三角形有3条对称轴,
D、正六边形有6条对称轴，
所以最少的是长方形．
故选：B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：（2x﹣1）2﹣2（x+3）（x﹣3）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一组数据23、20、20、21、26，这组数据的中位数和众数分别是（ ）
A. 21，20 B. 22，20 C. 21，26 D. 22，26
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列命题中是真命题的是
A．两边相等的平行四边形是菱形
B．一组对边平行一组对边相等的四边形是平行四边形
C．两条对角线相等的平行四边形是矩形
D．对角线互相垂直且相等的四边形是正方形
-
科目： 来源： 题型：
查看答案和解析>>【题目】(2016广东省梅州市第15题)如图，在平面直角坐标系中，将△ABO绕点A顺时针旋转到△AB1C1的位置，点B、O分别落在点B1、C1处，点B1在x轴上，再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置，点C2在x轴上，将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置，点A2在x轴上，依次进行下去…．若点A（
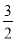，0），B（0，2），则点B2016的坐标为______________．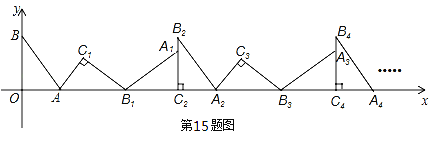
-
科目： 来源： 题型：
查看答案和解析>>【题目】(2016湖南省岳阳市第24题)如图①，直线y=
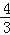x+4交于x轴于点A，交y轴于点C，过A、C两点的抛物线F1交x轴于另一点B（1，0）．（1）求抛物线F1所表示的二次函数的表达式；
（2）若点M是抛物线F1位于第二象限图象上的一点，设四边形MAOC和△BOC的面积分别为S四边形MAOC和S△BOC，记S=S四边形MAOC﹣S△BOC，求S最大时点M的坐标及S的最大值；
（3）如图②，将抛物线F1沿y轴翻折并“复制”得到抛物线F2，点A、B与（2）中所求的点M的对应点分别为A′、B′、M′，过点M′作M′E⊥x轴于点E，交直线A′C于点D，在x轴上是否存在点P，使得以A′、D、P为顶点的三角形与△AB′C相似？若存在，请求出点P的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】(2016重庆市第26题)如图1，二次函数
的图象与一次函数y=kx+b(k≠0)的图象交于A，B两点，点A的坐标为（0,1），点B在第一象限内，点C是二次函数图象的顶点，点M是一次函数y=kx+b(k≠0)的图象与x轴的交点，过点B作x轴的垂线，垂足为N，且S△AMO：S四边形AONB=1：48.（1）求直线AB和直线BC的解析式；
（2）点P是线段AB上一点，点D是线段BC上一点，PD//x轴，射线PD与抛物线交于点G，过点P作PE⊥x轴于点E，PF⊥BC于点F，当PF与PE的乘积最大时，在线段AB上找一点H（不与点A，点B重合），使GH+
BH的值最小，求点H的坐标和GH+BH的最小值；（3）如图2，直线AB上有一点K（3,4），将二次函数
沿直线BC平移，平移的距离是t(t≥0)，平移后抛物线使点A，点C的对应点分别为点A’，点C’；当△A’C’K是直角三角形时，求t的值。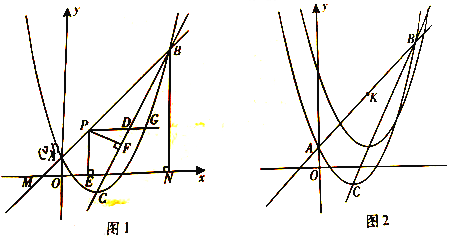
相关试题
