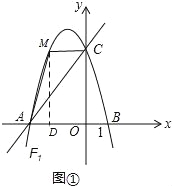
【题目】(2016湖南省岳阳市第24题)如图①,直线y=![]() x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
(1)求抛物线F1所表示的二次函数的表达式;
(2)若点M是抛物线F1位于第二象限图象上的一点,设四边形MAOC和△BOC的面积分别为S四边形MAOC和S△BOC,记S=S四边形MAOC﹣S△BOC,求S最大时点M的坐标及S的最大值;
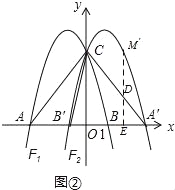
(3)如图②,将抛物线F1沿y轴翻折并“复制”得到抛物线F2,点A、B与(2)中所求的点M的对应点分别为A′、B′、M′,过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D、P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)、y=﹣![]() x2﹣
x2﹣![]() x+4;(2)、最大值为
x+4;(2)、最大值为![]() ;M(﹣
;M(﹣![]() ,5);(3)、(2,0)或(﹣
,5);(3)、(2,0)或(﹣![]() ,0)
,0)
【解析】
试题分析:(1)、利用一次函数的解析式求出点A、C的坐标,然后再利用B点坐标即可求出二次函数的解析式;(2)、由于M在抛物线F1上,所以可设M(a,﹣![]() a2﹣
a2﹣![]() a+4),然后分别计算S四边形MAOC和S△BOC,过点M作MD⊥x轴于点D,则S四边形MAOC的值等于△ADM的面积与梯形DOCM的面积之和;(3)、由于没有说明点P的具体位置,所以需要将点P的位置进行分类讨论,当点P在A′的右边时,此情况是不存在;当点P在A′的左边时,此时∠DA′P=∠CAB′,若以A′、D、P为顶点的三角形与△AB′C相似,则分为以下两种情况进行讨论:①
a+4),然后分别计算S四边形MAOC和S△BOC,过点M作MD⊥x轴于点D,则S四边形MAOC的值等于△ADM的面积与梯形DOCM的面积之和;(3)、由于没有说明点P的具体位置,所以需要将点P的位置进行分类讨论,当点P在A′的右边时,此情况是不存在;当点P在A′的左边时,此时∠DA′P=∠CAB′,若以A′、D、P为顶点的三角形与△AB′C相似,则分为以下两种情况进行讨论:①![]() =
=![]() ;②
;②![]() =
=![]() .
.
试题解析:(1)、令y=0代入y=![]() x+4, ∴x=﹣3, A(﹣3,0),
x+4, ∴x=﹣3, A(﹣3,0),
令x=0,代入y=![]() x+4, ∴y=4, ∴C(0,4),
x+4, ∴y=4, ∴C(0,4),
设抛物线F1的解析式为:y=a(x+3)(x﹣1),
把C(0,4)代入上式得,a=﹣![]() , ∴y=﹣
, ∴y=﹣![]() x2﹣
x2﹣![]() x+4,
x+4,
(2)、如图①,设点M(a,﹣![]() a2﹣
a2﹣![]() a+4) 其中﹣3<a<0 ∵B(1,0),C(0,4), ∴OB=1,OC=4
a+4) 其中﹣3<a<0 ∵B(1,0),C(0,4), ∴OB=1,OC=4
∴S△BOC=![]() OBOC=2, 过点M作MD⊥x轴于点D, ∴MD=﹣
OBOC=2, 过点M作MD⊥x轴于点D, ∴MD=﹣![]() a2﹣
a2﹣![]() a+4,AD=a+3,OD=﹣a,
a+4,AD=a+3,OD=﹣a,
∴S四边形MAOC=![]() ADMD+
ADMD+![]() (MD+OC)OD=
(MD+OC)OD=![]() ADMD+
ADMD+![]() ODMD+
ODMD+![]() ODOC=
ODOC=![]() +
+![]() =
=![]() +
+![]()
=![]() ×3(﹣
×3(﹣![]() a2﹣
a2﹣![]() a+4)+
a+4)+![]() ×4×(﹣a)=﹣2a2﹣6a+6
×4×(﹣a)=﹣2a2﹣6a+6
∴S=S四边形MAOC﹣S△BOC=(﹣2a2﹣6a+6)﹣2=﹣2a2﹣6a+4=﹣2(a+![]() )2+
)2+![]()
∴当a=﹣![]() 时, S有最大值,最大值为
时, S有最大值,最大值为![]() 此时,M(﹣
此时,M(﹣![]() ,5);
,5);
(3)、如图②,由题意知:M′(![]() ),B′(﹣1,0),A′(3,0) ∴AB′=2
),B′(﹣1,0),A′(3,0) ∴AB′=2
设直线A′C的解析式为:y=kx+b, 把A′(3,0)和C(0,4)代入y=kx+b,得:![]() ,∴
,∴
∴y=﹣![]() x+4, 令x=
x+4, 令x=![]() 代入y=﹣
代入y=﹣![]() x+4, ∴y=2 ∴
x+4, ∴y=2 ∴![]()
由勾股定理分别可求得:AC=5,DA′=![]() 设P(m,0)
设P(m,0)
当m<3时, 此时点P在A′的左边, ∴∠DA′P=∠CAB′, 当![]() =
=![]() 时,△DA′P∽△CAB′,
时,△DA′P∽△CAB′,
此时,![]() =
=![]() (3﹣m), 解得:m=2, ∴P(2,0)
(3﹣m), 解得:m=2, ∴P(2,0)
当![]() =
=![]() 时,△DA′P∽△B′AC, 此时,
时,△DA′P∽△B′AC, 此时,![]() =
=![]() (3﹣m) m=﹣
(3﹣m) m=﹣![]() , ∴P(﹣
, ∴P(﹣![]() ,0)
,0)
当m>3时, 此时,点P在A′右边, 由于∠CB′O≠∠DA′E, ∴∠AB′C≠∠DA′P
∴此情况,△DA′P与△B′AC不能相似,
综上所述,当以A′、D、P为顶点的三角形与△AB′C相似时,点P的坐标为(2,0)或(﹣![]() ,0).
,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中是真命题的是
A.两边相等的平行四边形是菱形
B.一组对边平行一组对边相等的四边形是平行四边形
C.两条对角线相等的平行四边形是矩形
D.对角线互相垂直且相等的四边形是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下面的图形中,对称轴条数最少的图形是( )
A.圆B.长方形C.正三角形D.正六边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016广东省梅州市第15题)如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(
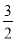 ,0),B(0,2),则点B2016的坐标为______________.
,0),B(0,2),则点B2016的坐标为______________.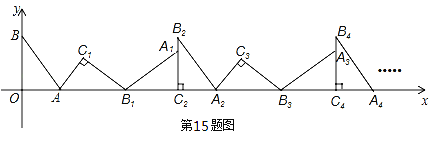
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016重庆市第26题)如图1,二次函数
 的图象与一次函数y=kx+b(k≠0)的图象交于A,B两点,点A的坐标为(0,1),点B在第一象限内,点C是二次函数图象的顶点,点M是一次函数y=kx+b(k≠0)的图象与x轴的交点,过点B作x轴的垂线,垂足为N,且S△AMO:S四边形AONB=1:48.
的图象与一次函数y=kx+b(k≠0)的图象交于A,B两点,点A的坐标为(0,1),点B在第一象限内,点C是二次函数图象的顶点,点M是一次函数y=kx+b(k≠0)的图象与x轴的交点,过点B作x轴的垂线,垂足为N,且S△AMO:S四边形AONB=1:48.(1)求直线AB和直线BC的解析式;
(2)点P是线段AB上一点,点D是线段BC上一点,PD//x轴,射线PD与抛物线交于点G,过点P作PE⊥x轴于点E,PF⊥BC于点F,当PF与PE的乘积最大时,在线段AB上找一点H(不与点A,点B重合),使GH+
 BH的值最小,求点H的坐标和GH+
BH的值最小,求点H的坐标和GH+ BH的最小值;
BH的最小值;(3)如图2,直线AB上有一点K(3,4),将二次函数
 沿直线BC平移,平移的距离是t(t≥0),平移后抛物线使点A,点C的对应点分别为点A’,点C’;当△A’C’K是直角三角形时,求t的值。
沿直线BC平移,平移的距离是t(t≥0),平移后抛物线使点A,点C的对应点分别为点A’,点C’;当△A’C’K是直角三角形时,求t的值。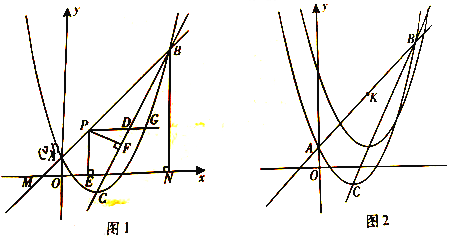
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学举行歌咏比赛,以班为单位参赛,评委组的各位评委给九年级三班的演唱打分情况(满分100分)如表,从中去掉一个最高分和一个最低分,则余下的分数的平均分是( )
分数(分)
89
92
95
96
97
评委(位)
1
2
2
1
1
A.92分
B.93分
C.94分
D.95分 -
科目: 来源: 题型:
查看答案和解析>>【题目】(2016山东省聊城市第29题)(1)、已知:△ABC是等腰三角形,其底边是BC,点D在线段AB上,E是直线BC上一点,且∠DEC=∠DCE,若∠A=60°(如图①).求证:EB=AD;
(2)、若将(1)中的“点D在线段AB上”改为“点D在线段AB的延长线上”,其它条件不变(如图②),(1)的结论是否成立,并说明理由;
(3)、若将(1)中的“若∠A=60°”改为“若∠A=90°”,其它条件不变,则
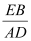 的值是多少?(直接写出结论,不要求写解答过程)
的值是多少?(直接写出结论,不要求写解答过程) 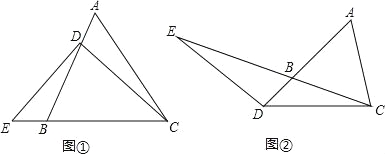
相关试题

