【题目】阅读下列材料: 如图1,圆的概念:在平面内,线段PA绕它固定的一个端点P旋转一周,另一个端点A所形成的图形叫做圆.就是说,到某个定点等于定长的所有点在同一个圆上,圆心在P(a,b),半径为r的圆的方程可以写为:(x﹣a)2+(y﹣b)2=r2 , 如:圆心在P(2,﹣1),半径为5的圆方程为:(x﹣2)2+(y+1)2=25
(1)填空: ①以A(3,0)为圆心,1为半径的圆的方程为;
②以B(﹣1,﹣2)为圆心, ![]() 为半径的圆的方程为 .
为半径的圆的方程为 .
(2)根据以上材料解决下列问题: 如图2,以B(﹣6,0)为圆心的圆与y轴相切于原点,C是⊙B上一点,连接OC,作BD⊥OC垂足为D,延长BD交y轴于点E,已知sin∠AOC= ![]() .
.
①连接EC,证明EC是⊙B的切线;
②在BE上是否存在一点P,使PB=PC=PE=PO?若存在,求P点坐标,并写出以P为圆心,以PB为半径的⊙P的方程;若不存在,说明理由.
参考答案:
【答案】
(1)(x﹣3)2+y2=1;(x+1)2+(y+2)2=3
(2)①证明:∵BD⊥OC,
∴CD=OD,
∴BE垂直平分OC,
∴EO=EC,
∴∠EOC=∠ECO,
∵BO=BC,
∴∠BOC=∠BCO,
∴∠EOC+∠BOC=∠ECO+∠BCO,
∴∠BOE=∠BCE=90°,
∴BC⊥CE,
∴EC是⊙B的切线;
②存在.
∵∠BOE=∠BCE=90°,
∴点C和点O偶在以BE为直径的圆上,
∴当P点为BE的中点时,满足PB=PC=PE=PO,
∵B点坐标为(﹣6,0),
∴OB=6,
∵∠AOC+∠DOE=90°,∠DOE+∠BEO=90°,
∴∠BEO=∠AOC,
∴sin∠BEO=sin∠AOC= ![]() ,
,
在Rt△BOE中,sin∠BEO= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴BE=10,
∴OE= ![]() =8,
=8,
∴E点坐标为(0,8),
∴线段AB的中点P的坐标为(﹣3,4),PB=5,
∴以P(﹣3,4)为圆心,以5为半径的⊙P的方程为(x+3)2+(y﹣4)2=25.
【解析】(1)解:①以A(3,0)为圆心,1为半径的圆的方程为(x﹣3)2+y2=1; ②以B(﹣1,﹣2)为圆心, ![]() 为半径的圆的方程为(x+1)2+(y+2)2=3;
为半径的圆的方程为(x+1)2+(y+2)2=3;
所以答案是(x﹣3)2+y2=1;(x+1)2+(y+2)2=3;
【考点精析】关于本题考查的等腰三角形的性质和勾股定理的概念,需要了解等腰三角形的两个底角相等(简称:等边对等角);直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】植树节来临之际,学校准备购进一批树苗,已知2棵甲种树苗和5棵乙种树苗共需113元;3棵甲种树苗和2棵乙种树苗共需87元.
(1)求一棵甲种树苗和一棵乙种树苗的售价各是多少元?
(2)学校准备购进这两种树苗共100棵,并且乙种树苗的数量不多于甲种树苗数量的2倍,请设计出最省钱的购买方案,并求出此时的总费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润不低于25%(不考虑其他因素),那么每件衬衫的标价至少是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.
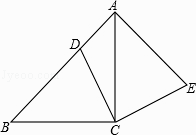
(1)求证:AB⊥AE;
(2)若BC2=ADAB,求证:四边形ADCE为正方形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c经过A(﹣3,0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO.
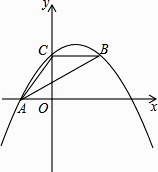
(1)求抛物线的解析式;
(2)线段AB上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;
(3)抛物线的对称轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交点为A(﹣3,0),与y轴交点为B,且与正比例函数y=
 x的图象交于点C(m,4).
x的图象交于点C(m,4).(1)求m的值及一次函数y=kx+b的表达式;
(2)观察函数图象,直接写出关于x的不等式
 x<kx+b的解集.
x<kx+b的解集.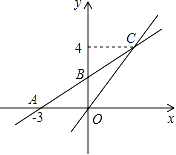
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,延长AB到点E,使BE=AB,连接DE交BC于点F,则下列结论不一定成立的是( )
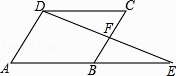
A.∠E=∠CDF
B.EF=DF
C.AD=2BF
D.BE=2CF
相关试题

