【题目】如图,△ABC为等边三角形,过点B作BD⊥AC于点D,过D作DE∥BC,且DE=CD,连接CE,
(1)求证:△CDE为等边三角形;
(2)请连接BE,若AB=4,求BE的长.

参考答案:
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)由△ABC为等边三角形得∠ACB=60°,又DE∥BC知∠EDC=60°,且DE=DC,从而可证△CDE为等边三角形;
(2)过点E作EH⊥BC于H,求出EH和CH的长,利用勾股定理即可求出BE的长.
试题解析:(1)∵△ABC为等边三角形
∴∠ACB=60°
∵DE∥BC
∴∠EDC=∠ACB=60°
又∵DE=DC
∴△CDE为等边三角形
(2)过点E作EH⊥BC于H
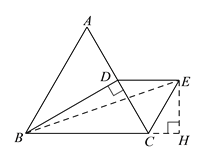
∵BD⊥AC ∴CD=![]() AC=
AC=![]() AB=2
AB=2
又∵△CDE为等边三角形
∴CE=CD=2
∵∠ECH=60°
∴EH=EC·sin60°=2×![]() =
=![]() ,CH=EC·cos60°=1
,CH=EC·cos60°=1
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的弦,点C为半径OA的中点,过点C作CD⊥OA交弦AB于点E,连接BD,且DE=DB.
(1)判断BD与⊙O的位置关系,并说明理由;
(2)若CD=15,BE=10,tanA=
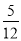 ,求⊙O的直径.
,求⊙O的直径.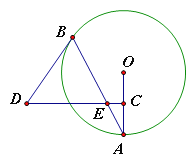
-
科目: 来源: 题型:
查看答案和解析>>【题目】某调查机构将今年温州市民最关注的热点话题分为消费、教育、环保、反腐及其它共五类.根据最近一次随机调查的相关数据,绘制的统计图表如下:

根据以上信息解答下列问题:
(1)本次共调查人________,请在补全条形统计图并标出相应数据________;
(2)若温州市约有900万人口,请你估计最关注教育问题的人数约为多少万人?
(3)在这次调查中,某单位共有甲、乙、丙、丁四人最关注教育问题,现准备从这四人中随机抽取两人进行座谈,求抽取的两人恰好是甲和乙的概率(列树状图或列表说明).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在洋浦一新开业的以经营男式皮鞋为主的鞋店当服务员的阿丽是个做事善于观察的小姑娘,上班一段时间后,她发现各种尺码的男式皮鞋销量并不均衡,于是她把这个发现记录下来交给了她的老板:
尺码
37
38
39
40
41
42
43
销量(双)
12
15
22
28
32
30
4
你认为这个销售记录对老板管理鞋店生意有用吗?如果你认为有用,请说明你的理由,并请你帮这个老板策划一下如何利用这些信息?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在以AB为直径的⊙O上,过C作⊙O的切线交AB的延长线于E,AD⊥CE于D,连结AC.
(1)求证:AC平分∠BAD.
(2)若tan∠CAD=
 ,AD=8,求⊙O直径AB的长.
,AD=8,求⊙O直径AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点(﹣1,m2+1)一定在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知2a-3b2=5,则10-2a+3b2的值是 ▲ .
相关试题

