Question

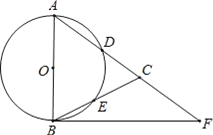
【题目】如图，在△ABC，AB=AC，以AB为直径的⊙O分别交AC、BC于点D、E，点F在AC的延长线上，且∠CBF=∠CAB．

（1）求证：直线BF是⊙O的切线；

（2）若AB=5，sin∠CBF=，求BC和BF的长．

Answer 1

【答案】（1）（2）见解析

【解析】（1）连接AE，利用直径所对的圆周角是直角，从而判定直角三角形，利用直角三角形两锐角相等得到直角，从而证明∠ABF=90°．

（2）利用已知条件证得△AGC∽△ABF，利用比例式求得线段的长即可．

（1）证明：连接AE，

∵AB是⊙O的直径，

∴∠AEB=90°，

∴∠1+∠2=90°．

∵AB=AC，

∴∠1=∠CAB．

∵∠CBF=∠CAB，

∴∠1=∠CBF

∴∠CBF+∠2=90°

即∠ABF=90°

∵AB是⊙O的直径，

∴直线BF是⊙O的切线．

（2）解：过点C作CG⊥AB于G．

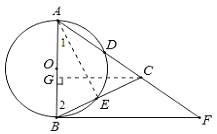
∵sin∠CBF=，∠1=∠CBF，

∴sin∠1=，

∵在Rt△AEB中，∠AEB=90°，AB=5，

∴BE=ABsin∠1=，

∵AB=AC，∠AEB=90°，

∴BC=2BE=2，

在Rt△ABE中，由勾股定理得AE==2，

∴sin∠2===，cos∠2===，

在Rt△CBG中，可求得GC=4，GB=2，

∴AG=3，

∵GC∥BF，

∴△AGC∽△ABF，

∴=．

∴BF==．