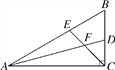
【题目】在直角△ABC中,∠ACB=90°,∠B=60°,AD,CE分别是∠BAC和∠BCA的平分线,AD,CE相交于点F.
(1)求∠EFD的度数;
(2)判断FE与FD之间的数量关系,并证明你的结论.
参考答案:
【答案】(1)120°;(2)FE=FD. 见解析
【解析】试题分析:(1)根据三角形内角和定理和角平分线的定义计算求解;
(2)在AC上截取AG=AE,则EF=FG;根据ASA证明△FGC≌△FDC,得DF=FG,故判断EF=FD.
试题解析:(1)∵△ABC中,∠ACB=90°,∠B=60°,
∴∠BAC=30°.
∵AD,CE分别是∠BAC和∠BCA的平分线,
∴∠FAC=![]() ∠BAC=15°,∠FCA=
∠BAC=15°,∠FCA=![]() ∠ACB=45°.
∠ACB=45°.
∴∠AFC=180°-∠FAC-∠FCA=120°,
∴∠EFD=∠AFC=120°.
(2)结论:FE=FD.
证明:如图,在AC上截取AG=AE,连接FG,
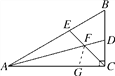
∵AD是∠BAC的平分线,
∴∠EAF=∠GAF.在△FAE和△FAG中,
AE=AG,∠EAF=∠GAF,AF=AF,
∴△AEF≌△AGF(SAS),
∴FE=FG,∠AFE=∠AFG.
∵∠EFD=120°,
∴∠DFC=60°,∠AFG=∠AFE=60°,
∴∠CFG=60°=∠DFC.
∵EC平分∠BCA,
∴∠DCF=∠FCG=45°.
在△FGC和△FDC中,
∵∠GFC=∠DFC,FC=FC,∠FCG=∠FCD,
∴△FGC≌△FDC(ASA),
∴FG=FD,
∴FE=FD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点(5,﹣3)所在的象限是___________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.
(1)求证:BE=CF;
(2)如果AB=8,AC=6,求AE、BE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若点M(a-3,a+4)在y轴上,则a=___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】8的立方根是( )
A.2B.土2C.士4D.﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠l=∠2,DE⊥BC,AB⊥BC,那么∠A=∠3吗?说明理由.

解:∠A=∠3,理由如下:
∵DE⊥BC,AB⊥BC(已知)
∴∠DEB=∠ABC=90° ( )
∴∠DEB+( )=180°
∴DE∥AB ( )
∴∠1=∠A( )
∠2=∠3( )
∵∠l=∠2(已知)
∴∠A=∠3( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们把a、b中较小的数记作min{a,b},设函数f(x)={2
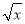 ,|x﹣2|}.若动直线y=m与函数y=f(x)的图象有三个交点,它们的横坐标分别为x1、x2、x3 , 则x1x2x3的最大值为________.
,|x﹣2|}.若动直线y=m与函数y=f(x)的图象有三个交点,它们的横坐标分别为x1、x2、x3 , 则x1x2x3的最大值为________.
相关试题

