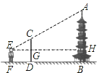
【题目】如图,小明欲测量一座古塔的高度,他拿出一根竹杆竖直插在地面上,然后自己退后,使眼睛通过竹杆的顶端刚好看到塔顶,若小明眼睛离地面![]() ,竹杆顶端离地面
,竹杆顶端离地面![]() ,小明到竹杆的距离
,小明到竹杆的距离![]() ,竹杆到塔底的距离
,竹杆到塔底的距离![]() ,求这座古塔的高度.
,求这座古塔的高度.
参考答案:
【答案】古塔的高度是![]() 米.
米.
【解析】
先根据小明、竹竿、古塔均与地面垂直,EH⊥AB可知,BH=DG=EF=1.6m,再小明眼睛离地面1.6m,竹杆顶端离地面2.4m求出CG的长,由于CD∥AB可得出△EGC∽△EHA,再根据相似三角形的对应边成比例可求出AH的长,进而得出AB的长.
∵小明、竹竿、古塔均与地面垂直,EH⊥AB,
∴BH=DG=EF=1.6m,EG=DF,GH=DB,
∵小明眼睛离地面1.6m,竹杆顶端离地面2.4m,
∴CG=CD-EF=2.4-1.6=0.8m,
∵CD∥AB,
∴△EGC∽△EHA,DF=2m,DB=33m,
∴![]() ,即
,即![]() ,
,
解得AH=14m,
∴AB=AH+BH=14+1.6=15.6m,
答:古塔的高度是15.6米.
-
科目: 来源: 题型:
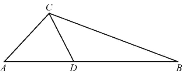
查看答案和解析>>【题目】经过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形,如果其中一个是等腰三角形,另外一个三角形和原三角形相似,那么把这条线段定义为原三角形的“和谐分割线”.如图,线段CD是△ABC的“和谐分割线”,△ACD为等腰三角形,△CBD和△ABC相似,∠A=46°,求∠ACB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC沿着DE对折,点A落到A′处,若∠BDA′+∠CEA′=70°,则∠A=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中有点A(0,1)、B(
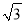 ,0).
,0).连接AB,以A为圆心,以AB为半径画弧,交y轴于点P1;
连接BP1,以B为圆心,以BP1为半径画弧,交x轴于点P2;
连接P1P2,以P1为圆心,以P1P2为半径画弧,交y轴于点P3;
按照这样的方式不断在坐标轴上确定点Pn的位置,那么点P6的坐标是_____.
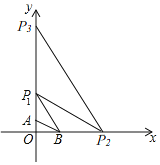
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解学生的安全意识情况,在全校范围内随机抽取部分学生进行问卷调查,根据查结果,把学生的安全意识分成淡薄、一般、较强、很强四个层次,并绘制成如下两幅尚不完整的统计图:

根据以上信息,解答下列问题:
(1)该校有1200名学生,现要对安全意识为淡薄、一般的学生强化安全教育,根据调查结果,估计全校需要强化安全教育的学生约有多少名?
(2)请将条形统计图补充完整.
(3)求出安全意识为“较强”的学生所占的百分比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知网格上最小的正方形的边长为
 (长度单位),点
(长度单位),点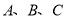 在格点上.
在格点上.(1)直接在平面直角坐标系中作出
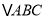 关于
关于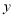 轴对称的图形
轴对称的图形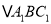 (点
(点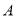 对应点
对应点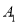 ,点
,点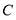 对应点
对应点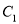 );
);(2)
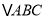 的面积为 (面积单位)(直接填空);
的面积为 (面积单位)(直接填空);(3)点
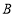 到直线
到直线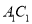 的距离为 (长度单位)(直接填空);
的距离为 (长度单位)(直接填空); 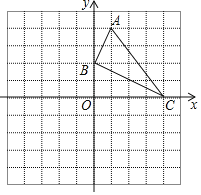
-
科目: 来源: 题型:
查看答案和解析>>【题目】小李在某商场购买
 两种商品若干次(每次
两种商品若干次(每次 商品都买) ,其中前两次均按标价购买,第三次购买时,
商品都买) ,其中前两次均按标价购买,第三次购买时, 商品同时打折.三次购买
商品同时打折.三次购买 商品的数量和费用如下表所示:
商品的数量和费用如下表所示:购买A商品的数量/个
购买B商品的数量/个
购买总费用/元
第一次
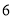
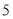

第二次


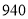
第三次
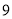

(1)求
 商品的标价各是多少元?
商品的标价各是多少元?(2)若小李第三次购买时
 商品的折扣相同,则商场是打几折出售这两种商品的?
商品的折扣相同,则商场是打几折出售这两种商品的?(3)在(2)的条件下,若小李第四次购买
商品共花去了
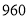 元,则小李的购买方案可能有哪几种?
元,则小李的购买方案可能有哪几种?
相关试题

