【题目】已知点O是等腰直角三角形ABC斜边上的中点,AB=BC,E是AC上一点,连结EB.
(1) 如图1,若点E在线段AC上,过点A作AM⊥BE,垂足为M,交BO于点F.求证:OE=OF;
(2)如图2,若点E在AC的延长线上,AM⊥BE于点M,交OB的延长线于点F,其它条件不变,则结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.

参考答案:
【答案】见解析
【解析】试题分析:(1)由三角形ABC是等腰直角三角形,AB=BC,得到∠BAC=∠ACB=45°,又由点O是AC边上的中点,得到∠BOE=∠AOF=90°,∠ABO=∠CBO=45°,从而得到∠BAC=∠ABO,OB=OA,又由AM⊥BE,得到∠MEA+∠MAE=90°=∠AFO+∠MAE,
故有∠MEA=∠AFO,得到Rt△BOE≌Rt△AOF,从而得到结论;
(2)同(1)可证明Rt△BOE≌Rt△AOF,从而得到OE=OF.
试题解析:(1)证明:∵三角形ABC是等腰直角三角形,AB=BC,
∴∠BAC=∠ACB=45°
又点O是AC边上的中点,
∴∠BOE=∠AOF=90°,∠ABO=∠CBO=45°
∴∠BAC=∠ABO,∴OB=OA,
又∵AM⊥BE,
∴∠MEA+∠MAE=90°=∠AFO+∠MAE,
∴∠MEA=∠AFO,
∴Rt△BOE≌Rt△AOF,∴OE=OF;
(2)OE=OF成立;
证明:∵三角形ABC是等腰直角三角形,AB=BC,
∴∠BAC=∠ACB=45°
又点O是AC边上的中点,
∴∠BOE=∠AOF=90°,∠ABO=∠CBO=45°
∴∠BAC=∠ABO,∴OB=OA,
又∵AM⊥BE,
∴∠F+∠MBF=90°=∠B+∠OBE,
又∵∠MBF=∠OBE,∴∠F=∠E,
∴Rt△BOE≌Rt△AOF,
∴OE=OF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】16的算术平方根和25的平方根的和是( )
A.9
B.-1
C.9或﹣1
D.﹣9或1 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,真命题的是( )
A.如果两个圆心角相等,那么它们所对的弧也相等
B.如果两个圆没有公共点,那么这两个圆外离
C.如果一条直线上有一个点到圆心的距离等于半径,那么这条直线与圆相切
D.如果圆的直径平分弧,那么这条直径就垂直平分这条弧所对的弦
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点P是第二象限内的点,且点P到x轴的距离是4,到y轴的距离是3,则点P的坐标是( )
A.(﹣4,3)
B.(4,﹣3)
C.(﹣3,4)
D.(3,﹣4) -
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,∠BAD的角平分线与边BC交于点E,∠ADC的角平分线交AE于点O,且点O在四边形ABCD的内部.
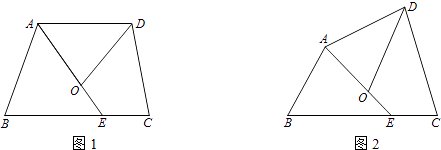
(1)如图1,若AD∥BC,∠B=70°,∠C=80°,则∠DOE=°.
(2)如图2,试探索∠B、∠C、∠DOE之间的数量关系,并将你的探索过程写下来 -
科目: 来源: 题型:
查看答案和解析>>【题目】今年春节黄金周上海共接待游客约5090000人,5090000这个数用科学记数法表示为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AB=15,AC=13,高AD=12,则△ABC中BC边的长为( )
A. 9 B. 5 C. 4 D. 4或14
相关试题

