Question

【题目】四边形ABCD中，∠BAD的角平分线与边BC交于点E，∠ADC的角平分线交AE于点O，且点O在四边形ABCD的内部．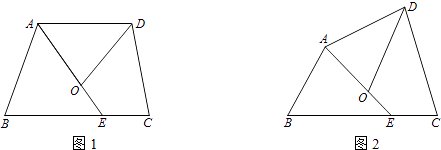
（1）如图1，若AD∥BC，∠B=70°，∠C=80°，则∠DOE=°．
（2）如图2，试探索∠B、∠C、∠DOE之间的数量关系，并将你的探索过程写下来

Answer 1

【答案】
（1）105
（2）解：∵∠DOE=∠OAD+∠ADO，

∵∠BAD的角平分线与边BC交于点E，∠ADC的角平分线交AE于点O，

∴2∠DOE=∠BAD+∠ADC，

∵∠B+∠C+∠BAD+∠ADC=360°，

∴∠B+∠C+2∠DOE=360°

【解析】解：（1）∵AD∥BC，∠B=70°，∠C=80°， ∴∠BAD=110°，∠ADC=100°，
∵∠BAD的角平分线与边BC交于点E，∠ADC的角平分线交AE于点O，
∴∠BAE=55°，∠ODC=50°，
∴∠AEC=125°，
∴∠DOE=360°﹣125°﹣80°﹣50°=105°；
所以答案是：105．
【考点精析】认真审题，首先需要了解平行线的性质(两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补)，还要掌握多边形内角与外角(多边形的内角和定理：n边形的内角和等于（n-2）180°.多边形的外角和定理：任意多边形的外角和等于360°)的相关知识才是答题的关键．