【题目】已知,点E、F分别在直线AB,CD上,点P在AB、CD之间,连结EP、FP,如图1,过FP上的点G作GH∥EP,交CD于点H,且∠1=∠2.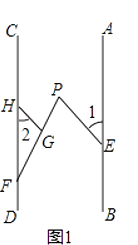
(1)求证:AB∥CD;
(2)如图2,将射线FC沿FP折叠,交PE于点J,若JK平分∠EJF,且JK∥AB,则∠BEP与∠EPF之间有何数量关系,并证明你的结论;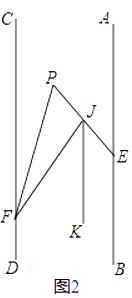
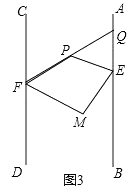
(3)如图3,将射线FC沿FP折叠,将射线EA沿EP折叠,折叠后的两射线交于点M,当EM⊥FM时,求∠EPF的度数.
参考答案:
【答案】
(1)
解:延长FP交AB于点Q,如图1,
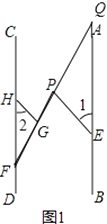
∵PE∥HG,
∴∠GPE=∠HGP,
∵∠GPE=∠1+∠PQE,∠HGP=∠2+∠HFG,
∵∠1=∠2,
∴∠PQE=∠HFG,
∴AB∥CD
(2)
解:延长FP交CD于点Q,如图2,
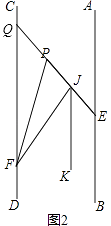
∠EPF+ ![]() ∠BEP=270°,理由如下:
∠BEP=270°,理由如下:
∵AB∥CD,
∴∠BEP+∠FQP=180°,
∵将射线FC沿FP折叠,
∴∠QFP=∠PFJ,
∵JK∥AB,
∴JK∥CD,
∴∠FJK=2∠CFP,
∵∠EPF=∠EQF+∠QFP,
∴∠EPF=180°﹣∠BEP+∠QFP,
∵JK平分∠EJF,
∴∠FJK=∠KJE,
∵JK∥CD,
∴∠KJE=∠FQP,
∴∠EPF=180°﹣∠BEP+ ![]() ∠FJK,
∠FJK,
∴∠EPF=180°﹣∠BEP+ ![]() ,
,
∴∠EPF+ ![]() ∠BEP=270°
∠BEP=270°
(3)
解:延长FP交AB于点Q,如图3,
∵AB∥CD,
∴∠CFQ=∠PQE,
∵将射线FC沿FP折叠,将射线EA沿EP折叠,
∴∠CFP=∠PFM,∠MEP=∠PEQ,
∵∠FPE=∠PQE+∠PEQ,
在四边形FPEM中,
∠PFM+∠MEP+∠FPE=360°﹣90°=270°,
可得:2∠FPE=270°,
∴∠FPE=135°
【解析】(1)延长FP交AB于点Q,根据三角形的外角性质和平行线性质证明即可;(2)延长FP交CD于点Q,根据折叠和平行线的性质解答即可;(3)延长FP交AB于点Q,根据折叠和四边形的内角和进行分析解答.
【考点精析】本题主要考查了平行线的判定与性质和翻折变换(折叠问题)的相关知识点,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.
-
科目: 来源: 题型:
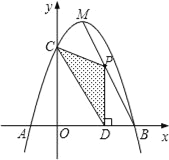
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c与x轴相交于A、B两点,与y轴相交于点C,且点B与点C的坐标分别为B(3,0).C(0,3),点M是抛物线的顶点.
(1)求二次函数的关系式;
(2)点P为线段MB上一个动点,过点P作PD⊥x轴于点D.若OD=m,△PCD的面积为S,试判断S有最大值或最小值?并说明理由;
(3)在MB上是否存在点P,使△PCD为直角三角形?如果存在,请求出点P的坐标;如果不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将直线y=-3x-2向上平移3个单位长度后得到的直线解析式是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市每天能出售甲、乙两种肉集装箱共21箱,且甲集装箱3天的销售量与乙集装箱4天的销售量相同.
(1)求甲、乙两种肉类集装箱每天分别能出售多少箱?
(2)若甲种肉类集装箱的进价为每箱200元,乙种肉类集装箱的进价为每箱180元,现超市打算购买甲、乙两种肉类集装箱共100箱,且手头资金不到18080元,则该超市有几种购买方案?
(3)若甲种肉类集装箱的售价为每箱260元,乙种肉类集装箱的售价为每箱230元,在(2)的情况下,哪种方案获利最多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x1=3y-2,x2=2y+4,则当y=____时,x1=x2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABD中,AB=AD,以AB为直径的⊙F交BD于点C,交AD与点E,CG⊥AD于点G.
(1)求证:GC是⊙F的切线;
(2)填空:①若△BCF的面积为15,则△BDA的面积为 .
②当∠GCD的度数为 时,四边形EFCD是菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,连接CD,C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )
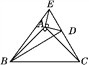
A. 1 B. 2 C. 3 D. 4
相关试题

