【题目】如图1,直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=8,BC=6,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP⊥AD于点P,连接AC交NP于点Q,连接MQ.设运动时间为t秒.

(1)AM= ,AP= .(用含t的代数式表示)
(2)当四边形ANCP为平行四边形时,求t的值
(3)如图2,将△AQM沿AD翻折,得△AKM,是否存在某时刻t,
①使四边形AQMK为为菱形,若存在,求出t的值;若不存在,请说明理由
②使四边形AQMK为正方形,则AC= .
参考答案:
【答案】(1)8﹣2t;2+t;(2)2;(3)①存在时刻t=1,使四边形AQMK为菱形.理由详见解析;②8![]() .
.
【解析】试题分析:(1)由DM=2t,根据AM=AD-DM即可求出AM=6-2t;先证明四边形CNPD为矩形,得出DP=CN=4-t,则AP=AD-DP=2+t;
(2)根据四边形ANCP为平行四边形时,可得4-t=6-(6=4-t),解方程即可;
(3))①由NP⊥AD,QP=PK,可得当PM=PA时有四边形AQMK为菱形,列出方程4-t-2t=6-(4-t),求解即可,
②要使四边形AQMK为正方形,由∠ADC=90°,可得∠CAD=45°,所以四边形AQMK为正方形,则CD=AD,由AD=8,可得CD=6,利用勾股定理求得AC即可.
试题解析:(1)6﹣2t,2+t.
(2)∵四边形ANCP为平行四边形时,CN=AP,
∴4﹣t=t+2,解得t=1,
(3)①∵NP⊥AD,QP=PK,
∴当PM=PA时有四边形AQMK为菱形,
∴4﹣t﹣2t=2+t,解得t=0.5,
∴存在时刻t=0.5,使四边形AQMK为菱形.
②AC=6![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若整式3x+5与4x-5的和为35,则x=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 半圆是弧,弧也是半圆 B. 三点确定一个圆
C. 平分弦的直径垂直于弦 D. 直径是同一圆中最长的弦
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我市教育行政部门为了了解七年级学生每学期参加综合实践活动的情况,随机抽样调查了某校七学生一个学期参加综合实践活动的天数,并用得到的数据绘制了如图两幅不完整的统计图.
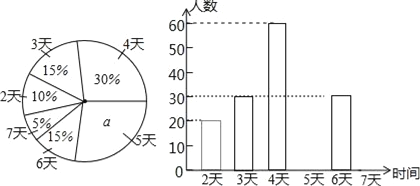
请你根据图中提供的信息,回答下列问题:
(1)求出扇形统计图中的a的值,并求出该校七年级学生总数;
(2)分别求出活动时问为5天、7天的学生人数,并补全频数分布直方图;
(3)求出扇形统计图中“活动时间为4天”的扇形所对圆心角的度数;
(4)如果该市共有七年级学生6000人,请你估计“活动时间不小于4天”的大约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,既是轴对称又是中心对称图形的是( )
A. 正方形B. 等边三角形C. 平行四边形D. 正五边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.-3(x-1)=-3x-1
B.-3(x-1)=-3x+1
C.-3(x-1)=-3x-3
D.-3(x-1)=-3x+3
相关试题

