【题目】一位农民带上若干千克自产的苹果进城出售.为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的苹果![]() (千克)与他手中持有的钱数
(千克)与他手中持有的钱数![]() (元)(含备用零钱)的关系如图,结合图象解决下列问题:
(元)(含备用零钱)的关系如图,结合图象解决下列问题:
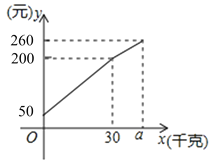
(1)农民自带的零钱是多少?
(2)求出降价前每千克的苹果价格是多少?
(3)降价后他按每千克![]() 元将剩余苹果售完,这时他手中
元将剩余苹果售完,这时他手中![]() 的钱(含备用零钱)是
的钱(含备用零钱)是![]() 元,试求出图象中
元,试求出图象中![]() 的值;
的值;
(4)求出降价前![]() 与
与![]() 之间的关系式(不要求写
之间的关系式(不要求写![]() 的取值范围).
的取值范围).
参考答案:
【答案】(1)50;(2)5;(3)45;(4)![]()
【解析】
(1)由图象可知,当x=0时,y=5,所以农民自带的零钱是5元.
(2)可设降价前每千克土豆价格为k元,则可列出农民手中钱y与所售土豆千克数x之间的函数关系式,由图象知,当x=30时,y的值,从而求出这个函数式.
(3)可设降价后农民手中钱y与所售土豆千克数x之间的函数关系式,因为当x=a时,y=260,当x=30时,y=200,依此列出方程求解.
(4)利用待定系数法求出0到30时线段的函数解析式即可.
(1)由图象可知,当![]() 时,
时,![]() .所以农民自带的零钱是
.所以农民自带的零钱是![]() 元.
元.
(2)降价前每千克苹果价格为:
![]() (元).
(元).
(3)降价后售出苹果的重量为:
![]() (千克).
(千克).
所以![]() .
.
(4)设![]() .根据题意,得
.根据题意,得
![]() .
.
![]()
将![]() 代入上式,得
代入上式,得![]() .
.
所以![]() 与
与![]() 的关系式为:
的关系式为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
 .
.(1)
 为何值时,
为何值时, 随
随 的增大而减小?
的增大而减小?(2)
 为何值时,函数图象与
为何值时,函数图象与 轴的交点在
轴的交点在 轴下方?
轴下方?(3)
 ,
, 分别是何值时,函数图象经过原点?
分别是何值时,函数图象经过原点?(4)当
 ,
, 时,求这个一次函数的图象与两个坐标轴的交点.
时,求这个一次函数的图象与两个坐标轴的交点. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店购进一批小玩具,每个成本价为20元,经调查发现售价为32元时,每天可售出20个,若售价每增加5元,每天销售量减少2个;售价每减少5元,每天销售量增加2个,商店同一天内售价保持不变.
(1)若售价增加
 元,则销售量是(______________)个(用含
元,则销售量是(______________)个(用含 的代数式表示);
的代数式表示);(2)某日商店销售该玩具的利润为384元,求当天的售价是多少元?(利润=售价-进价)
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于
 的方程
的方程 的所有根都是比1小的正实数,则实数
的所有根都是比1小的正实数,则实数 的取值范围是_______________.
的取值范围是_______________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明在大楼45米高(即PH=45米,且PH⊥HC)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的
坡度i(即tan∠ABC)为1:
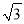 .(点P、H、B、C、A在同一个平面上
.(点P、H、B、C、A在同一个平面上点H、B、C在同一条直线上)
(1)∠PBA的度数等于________度;
(2)求A、B两点间的距离(结果精确到0.1米,参考数据:
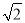 ≈1.414,
≈1.414, 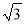 ≈1.732).
≈1.732).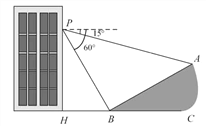
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三位数,十位上的数字是百位上数字的2倍,十位上的数字比个位上的数字大1.
(1)若设百位上的数字为a,则个位数字为 ,这个三位数可表示为 ;
(2)这个三位数能被5整除吗?若能,求出这个三位数;若不能请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题:
(1)3.587-(-5)+(-5
 )+(+7)-(+3
)+(+7)-(+3 )-(+1.587);
)-(+1.587);(2)(-1)5×{[-4
 ÷(-2)2+(-1.25)×(-0.4)]÷(-
÷(-2)2+(-1.25)×(-0.4)]÷(- )-32}.
)-32}.
相关试题

