【题目】如图,△ABC的面积为16,点D是BC边上一点,且BD= ![]() BC,点G是AB上一点,点H在△ABC内部,且四边形BDHG是平行四边形,则图中阴影部分的面积是( )
BC,点G是AB上一点,点H在△ABC内部,且四边形BDHG是平行四边形,则图中阴影部分的面积是( )
A.3
B.4
C.5
D.6
参考答案:
【答案】B
【解析】解:设△ABC底边BC上的高为h,△AGH底边GH上的高为h1 , △CGH底边GH上的高为h2 ,
则有h=h1+h2 .
S△ABC= ![]() BCh=16,S阴影=S△AGH+S△CGH=
BCh=16,S阴影=S△AGH+S△CGH= ![]() GHh1+
GHh1+ ![]() GHh2=
GHh2= ![]() GH(h1+h2)=
GH(h1+h2)= ![]() GHh.
GHh.
∵四边形BDHG是平行四边形,且BD= ![]() BC,
BC,
∴GH=BD= ![]() BC,
BC,
∴S阴影= ![]() ×(
×( ![]() BCh)=
BCh)= ![]() S△ABC=4.
S△ABC=4.
故选B.
【考点精析】关于本题考查的三角形的面积,需要了解三角形的面积=1/2×底×高才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.(写出一种即可)
关系:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°.
已知:在四边形ABCD中, , ;
求证:四边形ABCD是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处
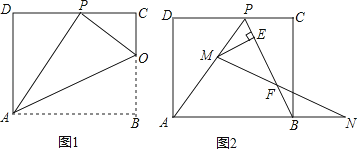
(1)如图1,已知折痕与边BC交于点O,连接AP、OP、OA.若△OCP与△PDA的面积比为1:4,求边CD的长.
(2)如图2,在(1)的条件下,擦去折痕AO、线段OP,连接BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E.试问当动点M、N在移动的过程中,线段EF的长度是否发生变化?若变化,说明变化规律.若不变,求出线段EF的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的不等式组
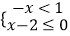 ,其解集在数轴上表示正确的是( )
,其解集在数轴上表示正确的是( )
A.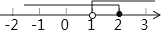
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为10,AG=CH=8,BG=DH=6,连接GH,则线段GH的长为( )

A.
B.
C.
D.10﹣5
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,直线
 ,E为AB、CD间的一点,连接EA、EC.
,E为AB、CD间的一点,连接EA、EC. 如图
如图 ,若
,若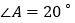 ,
, ,求
,求 的度数;
的度数; 如图
如图 ,若
,若 ,
, ,求
,求 的度数;
的度数; 如图
如图 ,若
,若 ,
, ,则
,则 ,
, 与
与 之间有何等量关系
之间有何等量关系 并简要说明.
并简要说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A,C在EF上,AD∥BC,DE∥BF,AE=CF.
(1)求证:四边形ABCD是平行四边形;
(2)直接写出图中所有相等的线段(AE=CF除外).

相关试题

