【题目】如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.(写出一种即可)
关系:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°.
已知:在四边形ABCD中, , ;
求证:四边形ABCD是平行四边形.

参考答案:
【答案】已知:①③(或①④或②④或③④),证明见解析.
【解析】试题分析:根据平行四边形的判定方法就可以组合出不同的结论,然后即可证明.
其中解法一是证明两组对角相等的四边形是平行四边形;
解法二是证明两组对边平行的四边形是平行四边形;
解法三是证明一组对边平行且相等的四边形是平行四边形;
解法四是证明两组对角相等的四边形是平行四边形.
试题解析:已知:①③,①④,②④,③④均可,其余均不可以.
解法一:
已知:在四边形ABCD中,①AD∥BC,③∠A=∠C,
求证:四边形ABCD是平行四边形.
证明:∵AD∥BC,
∴∠A+∠B=180°,∠C+∠D=180°.
∵∠A=∠C,
∴∠B=∠D.
∴四边形ABCD是平行四边形.
解法二:
已知:在四边形ABCD中,①AD∥BC,④∠B+∠C=180°,
求证:四边形ABCD是平行四边形.
证明:∵∠B+∠C=180°,
∴AB∥CD,
又∵AD∥BC,
∴四边形ABCD是平行四边形;
解法三:
已知:在四边形ABCD中,②AB=CD,④∠B+∠C=180°,
求证:四边形ABCD是平行四边形.
证明:∵∠B+∠C=180°,
∴AB∥CD,
又∵AB=CD,
∴四边形ABCD是平行四边形;
解法四:
已知:在四边形ABCD中,③∠A=∠C,④∠B+∠C=180°,
求证:四边形ABCD是平行四边形.
证明:∵∠B+∠C=180°,
∴AB∥CD,
∴∠A+∠D=180°,
又∵∠A=∠C,
∴∠B=∠D,
∴四边形ABCD是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知n边形的内角和θ=(n-2)×180°.
(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的面积为18,点D在线段AC上,点F在线段BC的延长线上,且
 ,四边形DCFE是平行四边形,则图中阴影部分的面积为( )
,四边形DCFE是平行四边形,则图中阴影部分的面积为( )
A. 8 B. 6 C. 4 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题6分)某市对一大型超市销售的甲、乙、丙3种大米进行质量检测.共抽查大米200袋,质量评定分为A、B两个等级(A级优于B级),相应数据的统计图如下:
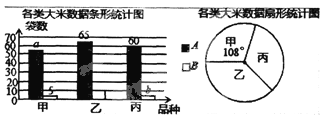
根据所给信息,解决下列问题:
(1)a=_______,b=_______.
(2)已知该超市现有乙种大米750袋,根据检测结果,请你估计该超市乙种大米中有多少袋B级大米?
(3)对于该超市的甲种和丙种大米,你会选择购买哪一种?请简述理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则GT=( )

A.
B.2
C.2
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC,直线PQ垂直平分AC,与边AB交于E,连接CE,过点C作CF平行于BA交PQ于点F,连接AF.
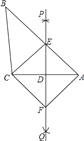
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为落实优秀传统文化进校园,某校计划购进“四书”、“五经”两套图书供学生借阅,已知这两套图书单价和为660元,一套“四书”比一套“五经”的2倍少60元.
(1)分别求出这两套图书的单价;
(2)该校购买这两套图书不超过30600元,且购进“四书”至少33套,“五经”的套数是“四书”套数的2倍,该校共有哪几种购买方案?
相关试题

