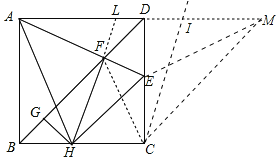
【题目】如图,正方形ABCD 中,AB=4,E为CD上一动点,连接AE交BD于F,过F作FH⊥AE于F,过H 作HG⊥BD 于 G.则下列结论:①AF=FH;②∠HAE=45°;③BD=2FG;④△CEH 的周长为 8.其中正确的个数是( )

A.1个B.2个C.3个D.4个
参考答案:
【答案】D
【解析】
①作辅助线,延长HF交AD于点L,连接CF,通过证明△ADF≌△CDF,可得:AF=CF,故需证明FC=FH,可证:AF=FH;
②由FH⊥AE,AF=FH,可得:∠HAE=45°;
③作辅助线,连接AC交BD于点O,证BD=2FG,只需证OA=GF即可,根据△AOF≌△FGH,可证OA=GF,故可证BD=2FG;
④作辅助线,延长AD至点M,使AD=DM,过点C作CI∥HL,则IL=HC,可证AL=HE,再根据△MEC≌△MIC,可证:CE=IM,故△CEH的周长为边AM的长.
①连接FC,延长HF交AD于点L,

∵BD为正方形ABCD的对角线,
∴∠ADB=∠CDF=45°.
∵AD=CD,DF=DF,
∴△ADF≌△CDF.
∴FC=AF,∠ECF=∠DAF.
∵∠ALH+∠LAF=90°,
∴∠LHC+∠DAF=90°.
∵∠ECF=∠DAF,
∴∠FHC=∠FCH,
∴FH=FC.
∴FH=AF.
②∵FH⊥AE,FH=AF,
∴∠HAE=45°.
③连接AC交BD于点O,可知:BD=2OA,

∵∠AFO+∠GFH=∠GHF+∠GFH,
∴∠AFO=∠GHF.
∵AF=HF,∠AOF=∠FGH=90°,
∴△AOF≌△FGH.
∴OA=GF.
∵BD=2OA,
∴BD=2FG.
④连接EM,延长AD至点M,使AD=DM,过点C作CI∥HL,则:LI=HC,
∵HL⊥AE,CI∥HL,
∴AE⊥CI,
∴∠DIC+∠EAD=90°,
∵∠EAD+∠AED=90°,
∴∠DIC=∠AED,
∵ED⊥AM,AD=DM,
∴EA=EM,
∴∠AED=∠MED,
∴∠DIC=∠DEM,
∴∠CIM=∠CEM,
∵CM=MC,∠ECM=∠CMI=45°,
∴△MEC≌△CIM,可得:CE=IM,
同理,可得:AL=HE,
∴HE+HC+EC=AL+LI+IM=AM=8.
∴△CEH的周长为8,为定值.
故①②③④结论都正确.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.

(1)求证:AD=AF;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.
-
科目: 来源: 题型:
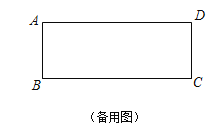
查看答案和解析>>【题目】在矩形ABCD中,AB=4,BC=10,E是直线AD上任意一点(不与点A重合),点A关于直线BE的对称点为A′,AA′所在直线与直线BC交于点F.
(1)如图①,当点E在线段AD上时,①若△ABE ∽△DEC,求AE的长;
②设AE=x,BF=y,求y与x的函数表达式.
(2)线段DA′的取值范围是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】《人民日报》2019年3月1日刊载了“2018年国民经济和社会发展统计公报”,有关脱贫攻坚的数据如下表。
年 度
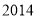
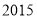
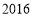
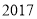
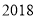
农村贫困人口/万
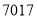
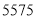
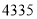
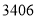
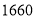
贫困发生率
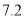
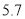
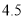
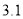
 在给出条形图中,直观表示今年农村贫困人口人数变化情况.
在给出条形图中,直观表示今年农村贫困人口人数变化情况. 根据你完善的统计图,写两点你获得的信息。
根据你完善的统计图,写两点你获得的信息。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,抛物线y=ax2-6ax+6(a≠0)与x轴交于点A(8,0),与y轴交于点B,在X轴上有一动点E(m,0)(0<m<8),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
,抛物线y=ax2-6ax+6(a≠0)与x轴交于点A(8,0),与y轴交于点B,在X轴上有一动点E(m,0)(0<m<8),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.(
 )分别求出直线AB和抛物线的函数表达式;
)分别求出直线AB和抛物线的函数表达式;(
 )设△PMN的面积为S1,△AEN的面积为S2,若S1:S2=36:25,求m的值;
)设△PMN的面积为S1,△AEN的面积为S2,若S1:S2=36:25,求m的值;(
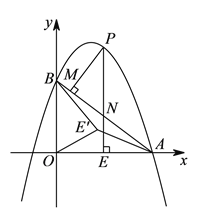
 )如图2,在(
)如图2,在(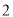 )条件下,将线段OE绕点O逆时针旋转得到OE',旋转角为α(0°<α<90°),连接E'A、E'B.
)条件下,将线段OE绕点O逆时针旋转得到OE',旋转角为α(0°<α<90°),连接E'A、E'B.①在x轴上找一点Q,使△OQE'∽△OE'A,并求出Q点的坐标;
②求BE'+
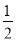 AE'的最小值.
AE'的最小值.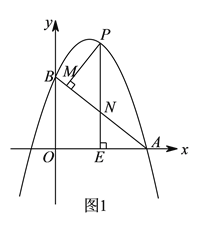
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( )
A. 一次函数y=﹣2x+3,y随x的增大而减小,
B. 反比例函数
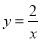 中,y随x的增大而增大,
中,y随x的增大而增大,C. 抛物线y=x2+1与y=x2﹣1的形状相同,只是位置不同,
D. 二次函数y=﹣2(x﹣2)2+3中,当x>2时,y随x的增大而减小
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,△ABC三个顶点的坐标分别是A(2,2)、B(2,0),C(4,2).

(1)在平面直角坐标系中画出△ABC;
(2)若将(1)中的△ABC平移,使点B的对应点B′坐标为(6,2),画出平移后的△A′B′C′;
(3)求△A′B′C′的面积.
相关试题

