Question

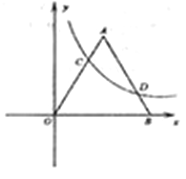
【题目】已知：如图，在平面直角坐标系中，等边的边长为6，点在边上，点在边上，且.反比例函数的图象恰好经过点和点.则的值为 （ ）

A． B． C. D．

Answer 1

【答案】A.

【解析】

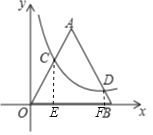
试题分析：过点C作CE⊥x轴于点E，过点D作DF⊥x轴于点F，设BD=a，则OC=3a，根据等边三角形的性质结合解含30度角的直角三角形，可找出点C、D的坐标，再利用反比例函数图象上点的坐标特征即可求出a、k的值，此题得解．

过点C作CE⊥x轴于点E，过点D作DF⊥x轴于点F，如图所示．

设BD=a，则OC=3a．

∵△AOB为边长为6的等边三角形，∴∠COE=∠DBF=60°，OB=6．

在Rt△COE中，∠COE=60°，∠CEO=90°，OC=3a，

∴∠OCE=30°，∴OE=a，CE=，∴点C（，）．

同理，可求出点D的坐标为（6﹣a，a）．

∵反比例函数（k≠0）的图象恰好经过点C和点D，

∴k=×a=（6﹣a）×a，∴a=，k=．

故选A．