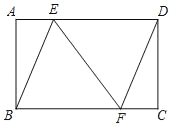
【题目】如图,在矩形ABCD中,点E,F分别是AD,BC边上的点,且AE=CF.
(1)求证:四边形BFDE是平行四边形;
(2)若AB=12,AE=5,cos∠BFE=![]() ,求矩形ABCD的周长.
,求矩形ABCD的周长.
参考答案:
【答案】(1)证明见解析(2)62
【解析】分析:(1)先求出![]() ,然后根据一组对边平行且相等的四边形是平行四边形证明四边形
,然后根据一组对边平行且相等的四边形是平行四边形证明四边形![]() 为平行四边形;
为平行四边形;
(2)由三角函数和勾股定理求出![]() ,得出
,得出![]() ,即可得出答案.
,即可得出答案.
详解:(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,AD=BC.AB=CD,
∵AE=CF,
∴DE=BF.
∴四边形BFDE是平行四边形。
(2)∵矩形ABCD,
∴![]()
过点E作EG⊥BC于G.
∵![]()
∴四边形ABGE是矩形,
∴AE=BG=5,AB=EG=12.
∵在Rt△EFG中,![]()
∴![]()
设FG=3x,EF=5x,
∴![]()
∴x=3.
∴FG=3x=9,
∴BC=BG+FG+CF=5+9+5=19.
∴矩形ABCD的周长=19×2+12×2=62.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有下列说法:①平行四边形既是中心对称图形,又是轴对称图形;②正方形有四条对称轴;③平行四边形相邻两个内角的和等于
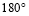 ;④菱形的面积计算公式,除了“
;④菱形的面积计算公式,除了“ 底×高”之外,还有“
底×高”之外,还有“ 两对角线之积”;⑤矩形和菱形均是特殊的平行四边形,因此具有平行四边形的所有性质.其中正确的结论的个数有( )
两对角线之积”;⑤矩形和菱形均是特殊的平行四边形,因此具有平行四边形的所有性质.其中正确的结论的个数有( )A. 1B. 2C. 3D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与直线CD相交于点O,EO⊥AB,OF平分∠AOC,
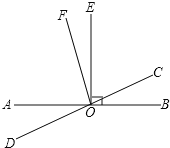
(1)请写出∠EOC的余角 ;
(2)若∠BOC=40°,求∠EOF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“一带一路”倡议提出3年多来,交通、通信、能源等各项相关建设取得积极进展,也为增进各国民众福祉提供了新的发展机遇.如图,是“一带一路”沿线部分国家的通信设施现状统计图.观察图,请回答下列问题:
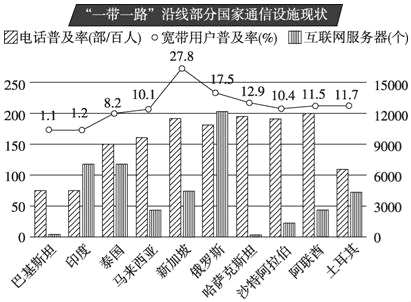
(1)在这10个国家中,互联网服务器拥有个数最多的国家是 ;
(2)在这10个国家中,每100人拥有电话数量最接近150部的国家是 ;
(3)在这10个国家中,宽带用户普及率最高的国家是 ,普及率为 ;
(4)在这10个国家中,宽带用户普及率的中位数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料
“一带一路”建设将以政策沟通、设施联通、贸易畅通、资金融通、民心相通为主要内容,为沿线国家发展和世界经济注入新动力.中国与“一带一路”沿线国家合作具有较好的基础.2012年中国与沿线国家的货物贸易额占中国货物贸易总额的24.8%,2013年中国与沿线国家的货物贸易额占中国货物贸易总额的25.0%.随着“一带一路”战略的实施,中国与“一带一路”沿线国家的贸易规模不断扩大,2014年,中国与沿线国家的货物贸易额达到1.12万亿美元,占中国货物贸易总额的26.1%.2015年,中国与沿线国家的货物贸易额达到0.93万亿美元,占中国货物贸易总额的25.3%.2016年,中国与沿线国家贸易额为0.95万亿美元,占中国货物贸易总额的25.7%.“一带一路”建设为我们打开了新思路,世界期待,为促进世界经济增长、深化地区合作打造更坚实的发展基础,更好地造福了各国人民.
根据以上材料解答下列问题:
(1)请你用统计图将2012﹣2016年中国与“一带一路”沿线国家的货物贸易额占中国货物贸易总额的百分比表示出来,并在图中标明相应数据;
(2)根据材料预估2017年中国与“一带一路”沿线国家贸易额约为 万亿美元,你估计的理由是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
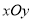 中,将一块含有
中,将一块含有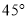 角的直角三角板如图放置,直角顶点
角的直角三角板如图放置,直角顶点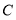 的坐标为
的坐标为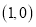 ,顶点
,顶点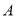 的坐标为
的坐标为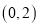 ,顶点
,顶点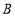 恰好落在第一象限的双曲线上,现将直角三角板沿
恰好落在第一象限的双曲线上,现将直角三角板沿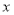 轴正方向平移,当顶点
轴正方向平移,当顶点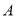 恰好落在该双曲线上时停止运动,则此时点
恰好落在该双曲线上时停止运动,则此时点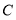 的对应点
的对应点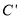 的坐标为( )
的坐标为( )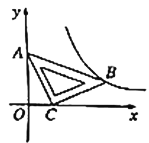
A.
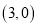 B.
B. 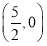 C.
C. 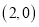 D.
D. 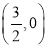
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形
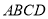 中,
中,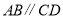 ,
,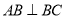 于点
于点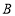 ,动点
,动点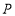 从点
从点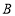 出发,沿
出发,沿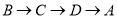 的方向运动,到达点
的方向运动,到达点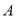 停止,设点
停止,设点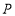 运动的路程为
运动的路程为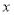 ,
,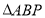 的面积为
的面积为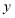 ,如果
,如果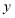 与
与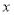 的函数图象如图2所示,那么
的函数图象如图2所示,那么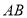 边的长度为______.
边的长度为______.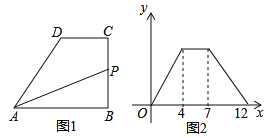
相关试题

