搜索
【题目】有下列说法：①平行四边形既是中心对称图形，又是轴对称图形；②正方形有四条对称轴；③平行四边形相邻两个内角的和等于
；④菱形的面积计算公式，除了“
底×高”之外，还有“两对角线之积”；⑤矩形和菱形均是特殊的平行四边形，因此具有平行四边形的所有性质.其中正确的结论的个数有（ ）
A. 1B. 2C. 3D. 4
参考答案：
【答案】C
【解析】
根据特殊平行四边形的性质即可判断.
①平行四边形既是中心对称图形，不是轴对称图形，故错误；②正方形有四条对称轴，正确；③平行四边形相邻两个内角的和等于
，正确；④菱形的面积计算公式，除了“
底×高”之外，还有“
两对角线之积”，故错误；⑤矩形和菱形均是特殊的平行四边形，因此具有平行四边形的所有性质，正确.
故②③⑤正确，选C
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知点C，D在线段AB上，M、N分别是AC、BD的中点，若AB=20，CD=4，
（1）求MN的长．
（2）若AB=a，CD=b，请用含有a、b的代数式表示出MN的长．
-
科目： 来源： 题型：
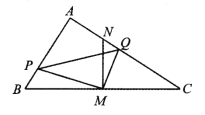
查看答案和解析>>【题目】在△ABC 中，∠BAC＝90°，AB<AC，M 是 BC 边的中点，MN⊥BC交 AC 于点 N，动点 P 在线段 BA 上以每秒
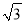cm 的速度由点 B 向点 A 运动．同时， 动点 Q 在线段 AC 上由点 N 向点 C 运动，且始终保持 MQ⊥MP． 一个点到终点时，两个点同时停止运动．设运动时间为 t 秒(t>0)．(1)△PBM 与△QNM 相似吗？请说明理由；
(2)若∠ABC＝60°，AB＝4
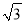cm．①求动点 Q 的运动速度；
②设△APQ 的面积为 s(cm2)，求 S 与 t 的函数关系式．（不必写出 t 的取值范围）
(3)探求 BP、PQ、CQ 三者之间的数量关系，请说明理由．
-
科目： 来源： 题型：
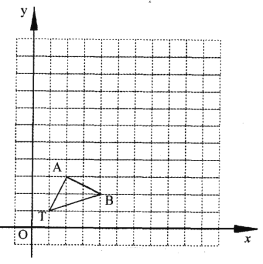
查看答案和解析>>【题目】如图，在正方形网格中，△TAB 的顶点坐标分别为 T(1，1)、A(2，3)、B(4，2)．
(1)以点 T(1，1)为位似中心，在位似中心的 同侧将△TAB 放大为原来的 3 倍，放大 后点 A、B 的对应点分别为 A'、B'，画出△TA'B'：
(2)写出点 A'、B'的坐标：A'( )、B'（ ）；
(3)在(1)中，若 C(a，b)为线段 AB 上任一 点，则变化后点 C 的对应点 C'的坐标为 ( )．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线AB与直线CD相交于点O，EO⊥AB，OF平分∠AOC，
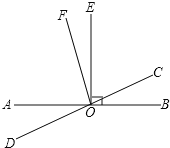
（1）请写出∠EOC的余角 ；
（2）若∠BOC＝40°，求∠EOF的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】“一带一路”倡议提出3年多来，交通、通信、能源等各项相关建设取得积极进展，也为增进各国民众福祉提供了新的发展机遇．如图，是“一带一路”沿线部分国家的通信设施现状统计图．观察图，请回答下列问题：
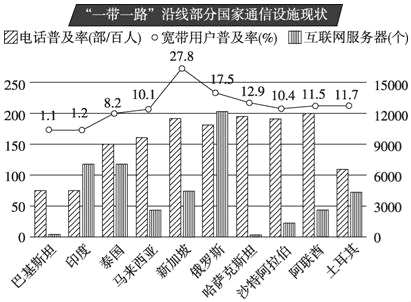
（1）在这10个国家中，互联网服务器拥有个数最多的国家是 ；
（2）在这10个国家中，每100人拥有电话数量最接近150部的国家是 ；
（3）在这10个国家中，宽带用户普及率最高的国家是 ，普及率为 ；
（4）在这10个国家中，宽带用户普及率的中位数是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，点E，F分别是AD，BC边上的点，且AE=CF．
（1）求证：四边形BFDE是平行四边形；
（2）若AB=12，AE=5，cos∠BFE=
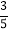，求矩形ABCD的周长．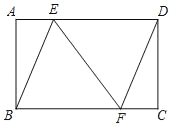
相关试题
