【题目】长为5,宽为![]() 的长方形纸片(
的长方形纸片(![]() ),如图那样翻折,剪下一个边长等于长方形宽度的正方形(成为第一次操作);再把剩下的长方形如图那样翻折,剪下一个边长等于此时长方形宽度的正方形(称为第二次操作);若在第3次操作后,剩下的图形为正方形,则
),如图那样翻折,剪下一个边长等于长方形宽度的正方形(成为第一次操作);再把剩下的长方形如图那样翻折,剪下一个边长等于此时长方形宽度的正方形(称为第二次操作);若在第3次操作后,剩下的图形为正方形,则![]() 的值为__________.
的值为__________.

参考答案:
【答案】3或![]()
【解析】
先根据题意可知:当![]() <a<20时,第一次操作后剩下的矩形的长为a、宽为5-a,第二次操作时正方形的边长为5-a,第二次操作以后剩下的矩形的两边分别为5-a、2a-5,然后分别从5-a>2a-5与5-a<2a-5去分析且列出一元一次方程求解即可得出正确答案.
<a<20时,第一次操作后剩下的矩形的长为a、宽为5-a,第二次操作时正方形的边长为5-a,第二次操作以后剩下的矩形的两边分别为5-a、2a-5,然后分别从5-a>2a-5与5-a<2a-5去分析且列出一元一次方程求解即可得出正确答案.
解:由题意可知:
当![]() <a<5时,
<a<5时,
第一次操作后剩下的矩形的长为a、宽为5-a,
∴第二次操作时剪下正方形的边长为5-a,
第二次操作以后剩下的矩形的两边分别为5-a、2a-5.
此时,分两种情况:
①如果5-a>2a-5,则a<![]() ,
,
即![]() <a<
<a<![]() ,
,
那么第三次操作时正方形的边长为2a-5.
则2a-5=(5-a)-(2a-5),
解得a=3;
②如果5-a<2a-5,则a>![]() ,
,
即![]() <a<20,
<a<20,
那么第三次操作时正方形的边长为5-a.
则5-a=(2a-5)-(5-a),
解得a=![]() .
.
∴当n=3时,a的值为3或![]() .
.
故答案为:3或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为
 ,C点的坐标为
,C点的坐标为 ,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着
,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着 的路线移动
的路线移动 即:沿着长方形移动一周
即:沿着长方形移动一周 .
. 写出点B的坐标
写出点B的坐标 ______
______
 当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标. 在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
(1)描出A(﹣4,3)、B(﹣1,0)、C(﹣2,3)三点.
(2)△ABC 的面积是多少?
(3)作出△ABC 关于 y 轴的对称图形.
(4)请在x 轴上求作一点P,使△PA1C1 的周长最小,并直接写出点P 的坐标

-
科目: 来源: 题型:
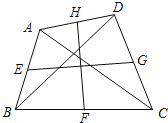
查看答案和解析>>【题目】如图,在四边形ABCD中,AC=BD=6,E、F、G、H分别是AB、BC、CD、DA的中点,则EG2+FH2=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠A=∠B=50°,P 为 AB 中点,点 M 为射线 AC 上(不与点 A 重合)的任意一点,连接 MP, 并使MP 的延长线交射线BD 于点N,设∠BPN=α.

(1)求证:△APM≌△BPN;
(2)当 MN=2BN 时,求α的度数;
(3)若△BPN 为锐角三角形时,直接写出α的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中描出下列各组点,并将各组内的点用线段依次连接起来.

(1,1),(3,1),(1,3),(1,1);
(-1,3),(-1,5),(-3,3),(-1,3);
(-5,1),(-3,-1),(-3,1),(-5,1);
(-1,-1),(1,-1),(-1,-3),(-1,-1).
(1)观察所得的图形,你觉得它像什么?
(2)求出这四个图形的面积和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图1菱形ABCD,∠ABC=60°,边长为 3,在菱形内作等边三角形△AEF,边长为2
 ,点E,点F,分别在AB,AC上,以A为旋转中心将△AEF顺时针转动,旋转角为α,如图2
,点E,点F,分别在AB,AC上,以A为旋转中心将△AEF顺时针转动,旋转角为α,如图2
(1)在图2中证明BE=CF;
(2)若∠BAE=45°,求CF的长度;
(3)当CF=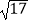 时,直接写出旋转角α的度数.
时,直接写出旋转角α的度数.
相关试题

