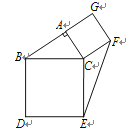
【题目】如图，在△ABC中，∠BAC＝90°，分别以AC，BC为边长，在三角形外作正方形ACFG和正方形BCED．若AC＝4，AB＝6，则EF＝______．

参考答案：

【答案】10

【解析】

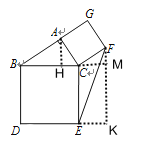
过点A作AH⊥BC，过点F作FK⊥DE交DE延长线于K，延长BC交FK于点M，根据勾股定理可求出BC，利用面积法可求出AH，再次利用勾股定理可求出HC，然后证明△AHC≌△CMF即可得到CM和MF的值，最后利用勾股定理求EF即可.

解：过点A作AH⊥BC，过点F作FK⊥DE交DE延长线于K，延长BC交FK于点M，

∵AC＝4，AB＝6，

∴BC=，

∵，

∴，

∴HC=，

∵FK⊥DK，BM∥DK，

∴FK⊥BM，即∠CMF=90°，

∴∠AHC=∠CMF=90°，∠MCF+∠CFM=90°，

∵∠MCF+∠HCA=90°，

∴∠CFM=∠HCA，

又∵AC=CF，

∴△AHC≌△CMF（AAS），

∴CM=AH=，MF=HC=,

∵∠CEK=∠ECM=∠CMK=90°，

∴四边形ECMK为矩形，

∴EK=CM=，FK=MF+MK=，

∴EF.

关闭