【题目】如图,在△ABC中,AB=AC,△ABC的高BH,CM交于点P.
(1)求证:PB=PC.
(2)若PB=5,PH=3,求AB.

参考答案:
【答案】(1)见解析;(2)10.
【解析】
(1)根据等边对等角可得∠ABC=∠ACB,根据三角形内角和定理可得∠MBP=∠HCP,然后可得∠PBC=∠PCB,可证PB=PC;
(2)利用AAS可直接证明△PMB≌△PHC,得到PM=PH=3,BM=CH,然后求出BM,在直角△ABH中利用勾股定理构建方程求出AM即可解决问题.
解:(1)∵AB=AC,
∴∠ABC=∠ACB,
又∵∠PMB=∠PHC=90°,∠MPB=∠HPC,
∴∠MBP=∠HCP,
∴∠ABC-∠MBP =∠ACB-∠HCP,即∠PBC=∠PCB,
∴PB=PC;
(2)在△PMB和△PHC中,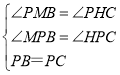 ,
,
∴△PMB≌△PHC(AAS),
∴PM=PH=3,BM=CH,
∴BM=![]() ,AM=AH,
,AM=AH,
在Rt△ABH中,AB2=AH2+BH2,
∴(4+AM)2= AH2+(5+3)2,即(4+AM)2= AM2+82,
解得:AM=6,
∴AB=AM+BM=6+4=10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AB=5,AC=4,∠B,∠C的平分线相交于点O,OM∥AB,ON∥AC分别与BC交于点M、N,则△OMN的周长为____.

-
科目: 来源: 题型:
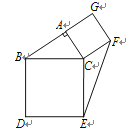
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,分别以AC,BC为边长,在三角形外作正方形ACFG和正方形BCED.若AC=4,AB=6,则EF=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为6 cm的等边三角形,动点P从A出发,以3 cm/s的速度,沿A-B-C向C运动,同时,动点Q从C出发沿CA方向以1 cm/s的速度向A运动,当其中一点运动到终点时,两点同时停止运动.设运动时间为t秒,当t= ____s,△APQ是直角三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果三角形有一边上的中线长恰好等于这边的长,那么这个三角形叫“恰等三角形”,这条中线叫“恰等中线”.
(直角三角形中的“恰等中线”)
(1)如图1,在△ABC中,∠C=90°,AC=
 ,BC=2,AM为△ABC的中线.求证:AM是“恰等中线”.
,BC=2,AM为△ABC的中线.求证:AM是“恰等中线”.
(等腰三角形中的“恰等中线”)
(2)已知,等腰△ABC是“恰等三角形”,AB=AC=20,求底边BC的平方.
(一般三角形中的“恰等中线”)
(3)如图2,若AM是△ABC的“恰等中线”,则BC2,AB2,AC2之间的数量关系为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在四边形ABCD中,AD∥BC,M为CD中点,AM平分∠DAB,AD+BC=AB.求证:BM平分∠ABC.

(1)请你简要叙述小淇证明方法的错误之处;
(2)若AB=5,AM=3,求四边形ABCD面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数
 的图象与
的图象与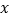 轴分别交于A(1,0),B(3,,0)两点,与
轴分别交于A(1,0),B(3,,0)两点,与 轴交于点C.
轴交于点C.(1)求此二次函数解析式;
(2)点D为抛物线的顶点,试判断
 的形状,并说明理由.
的形状,并说明理由.
相关试题

