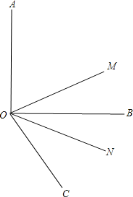
【题目】如图,射线![]() 在
在![]() 的外部,
的外部,![]() (
(![]() 为锐角)且
为锐角)且![]() 平分
平分![]() ,
,![]() 平分
平分![]() .
.
(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)若![]() (
(![]() 为锐角)不变,当
为锐角)不变,当![]() 的大小变化时,
的大小变化时,![]() 的度数是否变化?说明理由;
的度数是否变化?说明理由;
(3)从(1)(2)的结果来看你能看出什么规律.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ,理由见解析;(3)见解析.
,理由见解析;(3)见解析.
【解析】
(1)结合图形,根据角的和差,以及角平分线的定义,找到∠MON与∠AOB的关系,即可求出∠MON的度数;
(2)由(1)的结论可知∠MON=![]() ∠AOB,所以若∠AOB=β(β为锐角)不变,当∠BOC的大小变化时,∠MON的度数不变化,即∠MON=
∠AOB,所以若∠AOB=β(β为锐角)不变,当∠BOC的大小变化时,∠MON的度数不变化,即∠MON=![]() β;
β;
(3)从(1)(2)的结果来看,射线OC在∠AOB的外部,∠BOC=a(a为锐角)且OM平分∠AOC,ON平分∠BOC,若∠AOB=β(β为锐角)不变,当∠BOC的大小变化时,∠MON的度数不变化,即∠MON=![]() ∠AOB=
∠AOB=![]() β.
β.
![]() 因为
因为![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,
所以![]() ,
,![]() ,
,
所以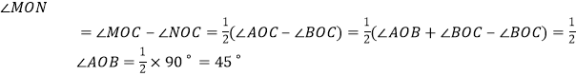 ;
;
![]() 由
由![]() 的结论可知
的结论可知![]() ,
,
所以若![]() (
(![]() 为锐角)不变,当
为锐角)不变,当![]() 的大小变化时,
的大小变化时,![]() 的度数不变化,即
的度数不变化,即![]() ;
;
![]() 从
从![]() 的结果来看,射线
的结果来看,射线![]() 在
在![]() 的外部,
的外部,![]() (
(![]() 为锐角)且
为锐角)且![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,若
,若![]() (
(![]() 为锐角)不变,当
为锐角)不变,当![]() 的大小变化时,
的大小变化时,![]() 的度数不变化,即
的度数不变化,即![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,等腰三角形ABO的底边OA在x轴上,顶点B在反比例函数y=
 (x>0)的图象上,当底边OA上的点A在x轴的正半轴上自左向右移动时,顶点B也随之在反比例函数y=
(x>0)的图象上,当底边OA上的点A在x轴的正半轴上自左向右移动时,顶点B也随之在反比例函数y=  (x>0)的图象上滑动,但点O始终位于原点.
(x>0)的图象上滑动,但点O始终位于原点.
(1)如图①,若点A的坐标为(6,0),求点B的坐标;
(2)当点A移动到什么位置时,三角形ABO变成等腰直角三角形,请说明理由;
(3)在(2)中,如图②,△PA1A是等腰直角三角形,点P在反比例函数y= (x>0)的图象上,斜边A1A在x轴上,求点A1的坐标.
(x>0)的图象上,斜边A1A在x轴上,求点A1的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】矩形ABCD中,点E、F分别在边CD、AB上,且DE=BF,∠ECA=∠FCA.
(1)求证:四边形AFCE是菱形;
(2)若AB=8,BC=4,求菱形AFCE的面积.

-
科目: 来源: 题型:
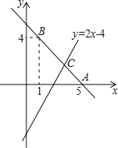
查看答案和解析>>【题目】已知直线y=kx+b经过点A(5,0),B(1,4).
(1)求直线AB的解析式;
(2)若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式2x﹣4>kx+b的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线l1经过点E(1,0)和F(5,0),并交y轴于D(0,﹣5);抛物线l2:y=ax2﹣(2a+2)x+3(a≠0),
(1)试求抛物线l1的函数解析式;
(2)求证:抛物线 l2与x轴一定有两个不同的交点;
(3)若a=1,抛物线l1、l2顶点分别为、;当x的取值范围是时,抛物线l1、l2 上的点的纵坐标同时随横坐标增大而增大;
(4)若a=1,已知直线MN分别与x轴、l1、l2分别交于点P(m,0)、M、N,且MN∥y轴,当1≤m≤5时,求线段MN的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(背景)某班在一次数学实践活动中,对矩形纸片进行折叠实践操作,并将其产生的数学问题进行相关探究. (操作)如图,在矩形ABCD中,AD=6,AB=4,点P是BC边上一点,现将△APB沿AP对折,得△APM,显然点M位置随P点位置变化而发生改变
(问题)试求下列几种情况下:点M到直线CD的距离
(1)∠APB=75°;
(2)P与C重合;
(3)P是BC的中点. -
科目: 来源: 题型:
查看答案和解析>>【题目】

(1)解方程: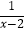 +
+  =2
=2
(2)如图,在⊙O中,OA⊥OB,∠A=20°,求∠B的度数.
相关试题

