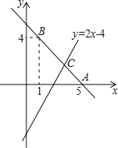
【题目】已知直线y=kx+b经过点A(5,0),B(1,4).
(1)求直线AB的解析式;
(2)若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式2x﹣4>kx+b的解集.
参考答案:
【答案】(1)y=-x+5;(2)点C(3,2);(3)x>3.
【解析】试题分析:(1)利用待定系数法把点A(5,0),B(1,4)代入y=kx+b可得关于k、b得方程组,再解方程组即可;
(2)联立两个函数解析式,再解方程组即可;
(3)根据C点坐标可直接得到答案.
试题解析:(1)∵直线y=kx+b经过点A(5,0),B(1,4),
∴![]() ,
,
解得![]() ,
,
∴直线AB的解析式为:y=-x+5;
(2)∵若直线y=2x-4与直线AB相交于点C,
∴![]() .
.
解得![]() ,
,
∴点C(3,2);
(3)根据图象可得x>3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两组数据:3,m,2n,5与m,6,n的平均数都是6,若将这两组数据合并为一组数据,求这组新数据的中位数、众数、方差.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的三个顶点A,B,C的坐标分别为A(4,0),B(0,-3),C(2,-4).

(1)在如图的平面直角坐标系中画出△ABC关于x轴对称的△A'B'C',并分别写出A′,B′,C′的坐标;
(2)将△ABC向左平移5个单位,请画出平移后的△A″B″C″,并写出△A″B″C″各个顶点的坐标;
(3)求出(2)中的△ABC在平移过程中所扫过的面积.
-
科目: 来源: 题型:
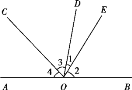
查看答案和解析>>【题目】如图,已知O为直线AB上一点,过点O向直线AB上方引三条射线OC、OD、OE,且OC平分∠AOD,∠2=3∠1.
(1)若∠1=18°,求∠COE的度数;
(2)若∠COE=70°,求∠2的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年以来,国务院连续发布了《关于加快构建大众创业万众创新支撑平台的指导意见》等一系列支持性政策,各地政府高度重视、积极响应,中国掀起了大众创业万众创新的新浪潮.某创新公司生产营销A、B两种新产品,根据市场调研,发现如下信息:
信息1:销售A种产品所获利润y(万元)与所售产品x(吨)之间存在二次函数关系y=ax2+bx,当x=1时,y=7;当x=2时,y=12.
信息2:销售B种产品所获利润y(万元)与所售产品x(吨)之间存在正比例函数关系y=2x.
根据以上信息,解答下列问题:
(1)求a,b的值;
(2)该公司准备生产营销A、B两种产品共10吨,请设计一个生产方案,使销售A、B两种产品获得的利润之和最大,最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线BC与半径为6的⊙O相切于点B,点M是圆上的动点,过点M作MC⊥BC,垂足为C,MC与⊙O交于点D,AB为⊙O的直径,连接MA、MB,设MC的长为x,(6<x<12).
(1)当x=9时,求BM的长和△ABM的面积;
(2)是否存在点M,使MDDC=20?若存在,请求出x的值;若不存在,请说明理由.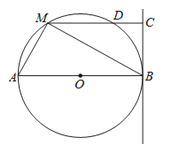
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B、C是数轴上的三点,O是原点,BO=3,AB=2BO,5AO=3CO.
(1)写出数轴上点A、C表示的数;
(2)点P、Q分别从A、C同时出发,点P以每秒2个单位长度的速度沿数轴向右匀速运动,点Q以每秒6个单位长度的速度沿数轴向左匀速运动,M为线段AP的中点,点N在线段CQ上,且CN=
 CQ.设运动的时间为t(t>0)秒.
CQ.设运动的时间为t(t>0)秒.①数轴上点M、N表示的数分别是 (用含t的式子表示);
②t为何值时,M、N两点到原点的距离相等?

相关试题

