【题目】综合与实践
问题解决:
如图1,已知正方形![]() ,
,![]() ,把含
,把含![]() (
(![]() )的直角三角板的一个锐角顶点和点
)的直角三角板的一个锐角顶点和点![]() 重合,三角板和正方形的
重合,三角板和正方形的![]() ,
,![]() 两边分别相交于
两边分别相交于![]() ,
,![]() 两点.
两点.
(1)当![]() 时,求
时,求![]() 的长;
的长;
探究发现:
(2)在图1的基础上,试探究![]() ,
,![]() ,
,![]() 有怎样的数量关系,请写出猜想,并给予证明.
有怎样的数量关系,请写出猜想,并给予证明.
类比延伸:
(3)如图2,若三角板和正方形![]() ,
,![]() 两边的延长线分别相交于
两边的延长线分别相交于![]() ,
,![]() 两点,请直接写出
两点,请直接写出![]() ,
,![]() ,
,![]() 存在的数量关系.
存在的数量关系.


参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;证明见解析;(3)
;证明见解析;(3)![]() .
.
【解析】
(1)直接利用勾股定理,即可求出AM的长度;
(2)延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() .先证明
.先证明![]() ,得到
,得到![]() ,然后得到
,然后得到![]() ,再证明
,再证明![]() ,即可得到结论成立.
,即可得到结论成立.
(3)在CN上截取CE=AM,连接ME,先证明△BCE≌△ABM,然后得到△MBE为等腰直角三角形,再根据垂直平分线的性质,线段的和差关系,即可得到结论.
解:(1)∵四边形![]() 为正方形,
为正方形,
∴![]() ,
,![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
(2)猜想:![]() .
.
证明:延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() .
.

在![]() 和
和![]() 中,
中,
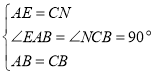 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
即![]() .
.
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)在CN上截取CE=AM,连接ME,

∵BC=AB,∠BAM=∠C=90°,
∴△BCE≌△BAM,
∴BE=BM,∠ABM=∠CBE,
∵∠MBN=45°,∠ABC=90°,
∴∠MBE=90°,△MBE为等腰直角三角形,
∴BN垂直ME,
∴BN为ME垂直平分线,
∴NM=NE.
∴CN-AM=CN-CE=NE=MN,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
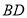 为
为 的一条对角线.
的一条对角线.(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母;(保留作图痕迹,不写作法)
①作
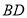 的垂直平分线
的垂直平分线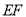 分别交
分别交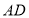 ,
,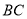 于
于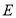 ,
,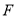 两点,交
两点,交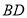 于点
于点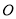 ;
;②连接
 ,
,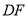 ;
;(2)猜想与证明:试猜想四边形
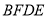 是哪种特殊的四边形,并说明理由.
是哪种特殊的四边形,并说明理由.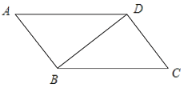
-
科目: 来源: 题型:
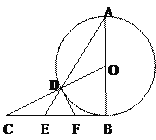
查看答案和解析>>【题目】如图:已知AB是⊙O的直径,BC是⊙O的切线,OC与⊙O相交于点D,连结AD并延长,与BC相交于点E。
(1)若BC=
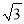 ,CD=1,求⊙O的半径;
,CD=1,求⊙O的半径; (2)取BE的中点F,连结DF,求证:DF是⊙O的切线。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.

(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=______度;
(2)设∠BAC=α,∠BCE=β.
①如图2,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,则α,β之间有怎样的数量关系?请直接写出你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC为直角三角形,∠ACB=90°,AB=5 cm,BC=3 cm,AC=4 cm,△ABC绕点C按逆时针方向旋转90°后得到△DEC,则∠D=______,∠B=________,DE=________cm,CE=______cm,AE=________cm,DB=________cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD的位置如图所示,解答下列问题:
(1)将四边形ABCD先向左平移4格,再向下平移6格,得到四边形A1B1C1D1,画出平移后的四边形A1B1C1D1;
(2)将四边形A1B1C1D1绕点A1逆时针旋转90°得到四边形A1B2C2D2,画出旋转后的四边形A1B2C2D2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某饮料经营部每天的固定成本为200元,其销售的饮料每瓶进价为5元.销售单价与日平均销售的关系如下:
销售单价(元)
6
6.5
7
7.5
8
8.5
9
日平均销售量(瓶)
480
460
440
420
400
380
360
(1)若记销售单价比每瓶进价多x元,则销售量为_____(用含x的代数式表示);
求日均毛利润(日均毛利润=(每瓶售价-每瓶进价)×日均销售量-固定成本)y与x之间的函数关系式.
(2)若要使日均毛利润达到1400元,则销售单价应定为多少元?
(3)若要使日均毛利润达到最大,销售单价应定为多少元?最大日均毛利润为多少元?
相关试题

